父の先見


産業図書 1995
Hao Wang
Reflections on Kurt Gödel
[訳]土屋俊・戸田山和久
ここのところ、ぼくの髭は伸びほうだいである。もともとたいして伸びない体質だからちょっとしか手を入れない。それでも"鶴仙人"のような髭になった。胃癌摘出のための入院中に伸ばしっぱなしにしたのを、そのまま1年近く放置したためだ。
そんな自分の髭を眺めていると、なぜ男は髭などはやすようになったのか、いや石器人や縄文人たちは髭を剃ることなど思いもつかなかったろうに、いつから剃る気になったのか、まったく妙な文化があったものだと、そんな変なことばかりを思いつく。そのうち、さきほど変わったことを思い出した。
髭については、こんなおかしなパラドクスがあるのだ。「床屋のパラドクス」というもので、こういう問題だ。「その村の床屋のAは、自分で髭を剃らない村人全員の髭を剃る。床屋のAも村人である。では、Aの髭を剃るのは誰なのか」。
試しに2分ばかり考えてみてほしい。どうだろうか。この問題をなんとか論理的につきつめようとすると、これまただんだん変な気分になる。たとえば、こういう具合だ。
もしAが床屋で自分の髭を剃ったのなら、Aは自分で髭を剃らない人物だということになるはずなのだが、それでは、その自分の髭を自分で剃ることになっておかしい。また、もしAは自分の髭を剃らないというのなら、Aは床屋ではなくなってしまって、やっぱりおかしい。この窮地を救うにはどう考えたらいいのか―。そういうパラドクスである。
これで変な気分にならないようなら、よっぽど論理学に強いか、論理実証主義のトレーニングをしたことがあるか、あるいはどんな理屈にも対応できないほどの"天然"か、もしくは何も考えられなかったか、こういうパズルが大嫌いか、そのどれかであるが、ふつうは気分が悪くなる。もっとも、これは髭のせいで変な気分になるのではない。パラドクスで変になる。
実は、このパラドクスの答えは「そんな床屋は存在しない」というものである。身長280センチの床屋が存在しないという意味で存在しないのではなく、論理的に存在しない。つまり、このメッセージは矛盾しているということなのだ。これが答えだ。
なんだ、そんなことかと憮然としたくなるだろうか。ほうら、やはり気分が悪くなったのではあるまいか。
パラドクスは気分を悪くさせるためにあるのではない。それなら、こんな面倒くさいものが何のためにあるかというと、人を迷わせるためではなく、メッセージ(情報)に言明(陳述)されたことの真偽を決めるにはどうすればいいのかということ、そのことを問いたいわけなのだ。
最もよく知られた有名なパラドクスに「クレタ人のパラドクス」がある。「すべてのクレタ人は嘘しか言わないと、クレタ人は言っている」というメッセージはウソかホントか、という問題だ。一度や二度は惑わされたろうが、答えは明白で、このメッセージはウソ(偽)の言明である。矛盾したメッセージなのだ。
ところがこういう言明を前に、われわれはしばしば右往左往する。まして、言明や陳述が科学的であったり数学的であったりするときは、ついつい信じたくなる。とくに数学的に立証されたと聞かされた定理や証明については、一も二もなく信じる気になっている。また、そう教えられてきた。たとえば「1+1=2」を誰も信じて疑わない。けれどもこれをメッセージ(言明)と見ると、この言明は「1+1は2である」というふうになって、この言明が真であるかを立証しようとするのが著しく困難なのである。
数学で証明されたことは正しい、とはかぎらない。数学が無矛盾であることを証明することは、できるまい。これがクルト・ゲーデルが到達した結論だった。
まったくとんでもない結論だった。「1+1は2である」という言明を矛盾なく立証するのは不可能だと言い出したのだ。それだけではなく、大半の数学は立証されるとはかぎらないと言い出した。つまりゲーデルは、数学には数学を立証する論理は含まれていないのではないかという爆弾宣言をしたのだった。
数学者は慌てた。数学者だけではなく科学者もギョッとした。とくに科学者は鼻白んで「そんな言いようはないだろう」という気になった。それならばまだしも、ずっとのちにスティーブン・ホーキングが物理学の統一理論に向かって掲げた次のような3つの選択肢のほうがホッとしたにちがいない。こういうものだ。
①最善のシナリオとは完全に正しい統一理論が完成することである。
②最悪のシナリオとは間違った統一理論が完成することである。
③次善のシナリオとは完全で正しい理論が完成しないことがわかることである。
さすがにホーキングらしい選択肢だが、このホーキングの選択肢でいえば、1931年にゲーデルが爆弾宣言で何をしたかは、はっきりしている。
①を否定して、「数学においては最善のシナリオはありえない」と断言したのである。これを「ゲーデルの第一不完全性定理」という。しかしそれならまだ、③の次善のシナリオが残っていると思うかもしれない。ふつうなら、そう思いたいだろう。けれどもしばらくして、ゲーデルは非情にも次の結論をくだした。「数学の理論が正しいと決まるなら、それを数学的に保証してみせることはできない」と。③もすげなく否定してしまったのだ。「ゲーデルの第二不完全性定理」というものだった。
話は髭のパラドクスどころではなくなったのである。
当時、数学界を牛耳っていたのはダヴィッド・ヒルベルトである。数学界に属する最俊英たちは、この帝王による「ヒルベルト計画」に一斉にとりくんでいた。この計画にはいろいろ細部はあるが、ごくおおざっぱにいえば、数学がけっして自己矛盾をおこさないことを証明しようという一大プロジェクトだった。多くの数学者が参加した。ヒルベルトの算段では「形式的理論」(これを純粋数学とも超数学ともいう)というものをつかえば、数学の無矛盾性は証明できるはずだったのだ。
形式的理論というのは、いってみれば写真のようなもので、数学を写真に撮ればそこに数学の自己矛盾を解決できる姿(論理)が写し出されるだろうというのである。ヒルベルトに師事していたフォン・ノイマンもこの考え方を確信していた。
ところが、1930年9月7日に古都ケーニヒスベルクで開かれた第2回科学認識論会議の最終日、24歳の青年が挙手をしてヒルベルトとノイマンの夢を打ち砕いた。ハンマーを持ってきた青年はゲーデルだった。ゲーデルは「形式的理論には数学を完全に写し出す力はない」と言い出したのだった。
驚いたノイマンが会議のあとこれをすぐさま精査してみたところ、どうも青年の言っていることは正しそうだ。天才的な才能という点ではゲーデルをはるかに上回るものを秘めていたであろうノイマンは、持ち前の集中力で「数学に矛盾がおきることを証明する手立てがないことを証明する論理式」をただちにまとめた。この証明はさすがに水際立ったものだったので、ノイマンはこれをゲーデル青年に教えてやろうと手紙を送った。ゲーデルからすぐに返信がきた。「すでにその証明は私が完璧に済ましています」という返信だ。数日前に「数学物理学雑誌」が受理したばかりの論文も同封されていた。ノイマンは愕然とする。
数学の自己矛盾は、一般にはパラドクスとして知られている。とくにゲオルグ・カントールが集合論を打ち立てて、そこから抽象数学を導き出してからは、集合論のパラドックスが頻繁に取り沙汰されるようになった。
最初に集合論パラドクスを発見したのはブラリ=フォルティだったのだが、有名になったのはバートランド・ラッセルによる「ラッセルのパラドクス」である。
そもそもカントールの集合論が独創的だったのは、集合が集まって別の集合になることもありうることを示したことにある。カントールは「集合の集合」がありうることを示した。たとえば{2,4,6,8‥}といった偶数の集合には偶数という要素が並んでいる。これをミカンに見立てれば、ミカンの房が要素で、ミカンの皮が集合になる。{2,4,6,8‥},{1,3,5,7,9‥}では、ミカンの房に偶数の集合と奇数の集合があって、それを大きなミカンが包んでいる。
このように要素と集合の関係を考えると、或る集合が別の集合の要素になるということはいくらでもおこりうることがわかる。そういう集合のミカンの皮を剥いてみると、そこには同じ集合が入っているということもありうる。
しかし、そのようにすると、「自分自身を集合の要素とする集合」では、ミカンを剥いても剥いても同じ集合が出てくることになってしまいかねない。こういう「自分自身を集合の要素とする集合」を悪性集合とし、そうでないものを良性集合とよぶとすると、ラッセルはもし数学が悪性集合を取り除けないなら、数学の将来はあやしいもんだと考えた。一方、ヒルベルトはその逆で、いや、数学は悪性集合のパラドクスも解けるし、必ず説明もつくと考えた。ノイマンもそういう一人だった。
だが、これらの望みをゲーデルがハンマーの一振りで打ち砕いたのである。
従来の数学的論理はアリストテレスの演繹的推論を基礎に築かれてきた。「もしすべてのXがYで、ZがXならば、ZはYである」というものだ。たいていの数理性はこの論理のうえに成り立っている。
これをわかりやすくしたのが、次の推論である。前提A「人間はみんな死ぬ」、前提B「K君は人間である」、ならば結論Cは「K君は死ぬ」となる。このような推論は「AとBが真実ならばCも真実になる」ということをあらわしている。もうすこしちゃんといえば、Aの陳述とBの陳述が真ならばCも真の陳述をもつはずである。そう決めたのだ。
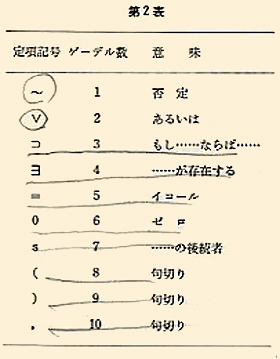
アリストテレスが打ち立てた論理の記述法を基盤として、その後、次々に推論のための論理の組み立てがつくられていった。19世紀の終盤になると、ゴットフリート・フレーゲらが登場してこれを数学的な数式に対応できる論理式にまで高めていった。そのための簡潔な論理記号も考案された。基本的な論理記号は「ならば」「かつ」「または」「でない」「同値」5種類からなっていて、これらを組み合わせて(ほかにもあるが)、数学的証明を論理記号による論理式だけで記述しようとしたのである。ちなみに5つの基本的な論理記号は、「ならば‥⊃」「かつ‥∧」「または‥∨」「でない‥¬」「同値‥≡」というふうになる。記号論理学はこういう論理記号を駆使しはじめたのだ。
こうして記号論理学が誕生していくのだが、しばらくして意外な問題が出てきた。ホワイトヘッドとともに記号論理学の体系をつくろうとしていたラッセルが、論理式では解けないパラドキシカルな問題があることに気がついたのだ。
これはパラドクスと純粋数学と論理学とが本気で出会った最初の本格的な事件だった。「AとBが真実ならばCも真実になる」という盤石の論理に、ヒビが入ったのだ。
ラッセルが気がついたパラドクスは「自分」が含まれているパラドクスだった。これを論理学では「自己言及する言明」というのだが、そのようなパラドキシカルな言明がいくつも発見されてしまった。そのうちのひとつとして冒頭に紹介した「髭のパラドックス」があったわけである。
では、自分を含む論理を数学や論理学は実証できないというのだろうか。ラッセルはその先のことまで手がつかなかったし、ヒルベルトはその逆の可能性を信じていたのだが、ゲーデルは手をつけた。そして冷たくも、「できない!」と断言した。
いったいゲーデルは何をしてみせたのか。
ゲーデルが「数学の無矛盾性を証明することができない」と断言したということは、その「証明することができない」ということを証明してみせたということである。えっ、そんなことができるのかと思いたいところだが、できたのだ。そこがゲーデルが巧妙だったところである。「ゲーデル数」という勝手な翻訳記号群と独自のルールをつくって、それを巧みに操作して「証明不能」を証明してみせた。
どのように証明してみせたのかを説明するのは、容易ではない。理論的に難解なのではなく、手続きが数理的であり、その途中に論理的な翻訳の手続きと自己言及の処理の手続きとが何度か介在するため、結論は簡単なのに、そのプロセスがめんどうくさい。ようするに論理計算につきあい、その論理計算の意表をつく翻訳につきあう必要があるからだ。
それでもとりあえずは、ゲーデルが何をしたか、ざっとその手続きを以下に集約しておくが、これを読んだところでさっぱり見当がつかないだろうとおもう。まあ、試みておく。
第1段階として、大前提の作業のことをいっておくと、ゲーデルはラッセルとホワイトヘッドの『プリンキピア・マテマティカ』を相手どったのである。
ラッセルとホワイトヘッドが何をしたかというと、ごくごく縮めていえば、「1+1は2である」を完全な論理式に移し変えるという作業を展示した。論理式に移し変えたというのは、さきほども書いたとおり、「すべて」「存在する」「ならば」「でない」「かつ」「または」といった論理記号だけによって、"算術"の意味をことごとく論理化したということである。そのうえで、パラドックスが論理的に証明できないことを示そうとした。
これを読んだ青年ゲーデルは、論理式によって数学の無矛盾が証明できないなら、実は数学そのものが数学的にも無矛盾を証明できないシステムになっているのではないかと考えた。
そこで第2段階、ゲーデルは『プリンキピア・マテマティカ』のなかのあらゆる論理式を自然数に戻してしまおうという計画をおもいついた。いわば論理式を鏡に写して書き直してみようと考えたのだ。写真にとるのではなく、鏡に写した。どう書き直すのか。第3段階、ゲーデルは論理式を鏡に映すにあたって「ゲーデル数」という符号群を導入してみた。そうすればゲーデル数によって、論理式は自然数の並び方に変換できる。鏡に映せる。
一方、第4段階、ゲーデルはエピメニデスの「クレタ人」のパラドックスにもとづく「この文はウソである」を根本的な例文にして、このパラドックスをめぐる真偽の証明が「可能である」と陳述したい文章があるとしたとき、その文章は「この陳述は証明不可能である」という意味(言明)になるような"仕掛け"をつくった。
この第4段階については、そもそもエピメニデスのパラドックスにどんな重要性(根本的な例になりうるということ)があるのかがわからないと、なぜそんなことをするのが有効なのか、まったく掴めないだろうが、それは本書や他のゲーデル解説書や論理学の本を読んで理解してもらうことにする。
こうして第5段階、ゲーデルは論理式をゲーデル数で変換したもの、これを「ゲーデル文」というのだが、そのゲーデル文の定義と証明にとりかかる。ゲーデル文は「この陳述は証明不可能である」という意味(言明)を含むという定義と証明である。
第6段階、ゲーデル文は、以上の形式的な手続きが無矛盾であったなら、真になるはずだということを証明できることを証明した。また第7に、仮にこのようにして生まれた証明の系に対して、別の新たな公理のようなものが加わったとしても、その公理をもつ新たな系もまたそれ自身の証明不可能なゲーデル文をもってしまうことを、証明した。
これでだいたいのところができあがった。かくて第8段階、ゲーデルはこれらのゲーデル文によって「数学は無矛盾である」という陳述をつくり、この陳述が証明できないことを示した。すべての準備がこれで終わった。
最後の第9段階、ゲーデルは「いっさいの形式体系としての数学は自身の無矛盾性を証明することは不可能である」と宣言した!
ゲーデルの証明は”手続き”だけの証明である。"手続き"だけを示した。だからこそ数学の無矛盾性という牙城を崩してきた。まことに天才的な魔術のようなものだ。
では、ゲーデルはどうしてこんなことを思いついたのか。これから少々スケッチするのは、ゲーデルがこのような発想にいたった背景と環境をめぐってみることである。
その前に本書について一言いっておくと、本書はすばらしいゲーデル解説になっている大著であるけれど、ゲーデル理論の最良の解説書とはいえない。ぼくが今夜書いていることも本書にのみ依拠していない。これまで渉猟してきた十数冊からのヒントにもとづいている。著者のハオ・ワンは長らくロックフェラー大学の論理学教授をつとめながら、1960年代からゲーデルと親交して、ゲーデルに招かれてプリンストン高等研究所の仕事を兼任した。ゲーデルの肉声のようなものを最もよく伝えているのが本書だったので、ゲーデル関連の代表書として選んだ。
ゲーデルの故郷はオーストリー=ハンガリー二重帝国のなかのモラヴィアの首都ブルンである。1906年に生まれた。
ブルンは、生物学者グレゴール・メンデル、物理学者エルンスト・マッハ、建築家アドルフ・ロース、設計者ヨーゼフ・ホフマンの故郷でもある(現在はチェコの都市になっている)。これだけでもとんでもない暗合を感じられるのだが、そのうえ、もともとこの都市には、ユダヤ教の伝統と異文化の香りとヤコブ・ベーメの神秘主義と、そしてドイツの論理と哲学とが入り交じっていた。
ゲーデルはここで育って、病気がちではあったものの、ギムナジウムで思う存分に勉学に熱中したようだ。ドイツ語・フランス語・英語を体得し、ギリシア語・ラテン語・イタリア語をほぼ解読できるようになっている。ぼくには速記術(ガベルスベルガー速記法)をマスターしようとしていたことも気になる。速記術はキケロこのかた言述の構造に関心をもった者たちが異常に活用しようとした”手続きの道具”であったからだ。時代はまさにユーゲント・シュティールの勃興期にあたる。
1924年、青年となったゲーデルはウィーン大学に進んだ。最初は宇宙や量子のことを解明したくて物理学科をえらんでいるが、半身不随の数学教授フィリップ・フルトヴェングラーに出会って、震撼した。その影響で、数学科に転向する。フルトヴェングラーは指揮者のフルトヴェングラーの従兄弟にあたる。
こういう事情があったせいか、このころゲーデルの数学知識ははやくも教授並に達していたようだ。
そのころのウィーン大学には、ウィーン学団の熱気が急速に沸騰しつつあった。ウィーン学団とはマッハの思想を普及することを目的としていたサークルの別名で、数学教授ハンス・ハーン、科学哲学者のシュリックが創立した。ウィーン9区シュトゥルデルホーフ小路にある数学研究所を根城に、ここで1924年から1936年までの12年間、毎週木曜の夕方6時から欠くことのない議論が連打された。
ゲーデルはこのシュリック・サークルに格別な関心をもつ。あげく、サークルの指導者モーリッツ・シュリックこそがゲーデルの最初の先生となった(あとで紹介するけれど、シュリックには劇的な最後が待っていた)。
そこにはシュリックだけでなく、カール・メンガー、フィリップ・フランク、オットー・ノイラート、のちに同僚となるルドルフ・カルナップがいた。つねに客分としてかかわっていたのはカール・ポパーとヴィトゲンシュタインと先輩格のボルツマンだった。ノイマンやアルフレッド・タルスキーも時々顔を見せている。
これだけの錚々たる顔ぶれである。たちまち世界を驚かせる多くの仮説が次々に湧き出て、ウィーン学団とシュリック・サークルの名はすぐさま天下に轟いた。青年ゲーデルはその渦中に一気に飛びこんでいったのだ。そして飛びこむと同時にあっというまに一つの確信に達した。その一つの確信こそ、ゲーデルに不完全性定理を思いつかせた原動力である。
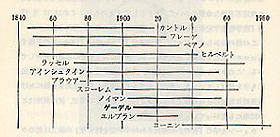
ウィーン学団の影響は世界中に飛び火した。たとえばライヘンバッハのベルリン学派、たとえばポーランド学派やウプサラ学派、あるいはラッセルやヴィトゲンシュタインのケンブリッジ学派、さらにはアメリカのプラグマティズムとも結びつき、しだいに分析哲学や人工言語学派の巨大なうねりともなっていった。
こんな波及力をもったウィーン学団の成果をここにのべはじめるとキリがない。ボルツマンの熱力学的原子論とヴィトゲンシュタインの論理的原子論だけでも衝撃的なのに、そこにノイラートとカルナップが「あらゆる命題は物理学の言語で書きなおせるはずだ」と言い出して、だれもかれもが「論理」だけで自然科学の全領域を語ろうという勢いだったのだ。のちにウィーン学団が論理実証主義の巣窟だったとみなされたのは、この「論理」好みに由来する。
しかし、ウィーン学団の独自性は論理実証主義にはとどまらないとも言うべきだ。もともと1895年にエルンスト・マッハがウィーン大学に「帰納的科学の歴史と理論」という講座を新設したのが嚆矢だったのである。それがボルツマンに引き継がれ、それをシュリックが引き継いだ。そこへ哲学者や社会学者が次々に参入していった。この領域の越境性だけからもあらかた見当がつくだろうように、この「知の巣窟」は物理学・熱力学・数学・社会学・言語学をすべて一つの坩堝に投げこんで、そこから来たるべき"統一科学"の論理そのものをさぐろうとしていた。まさに当代随一の過激な知的ムーブメントの武器庫のようなものであったのだ。
ぼくが思うには、このムーブメントの根底にあった「論理」とは、言及できるものと言及できないものを峻別して、言説にひそむであろう真のコンファーマビリティをひたすら実感しようというところにある。
言及の確証可能性(コンファーマビリティ)を"実感"するというのは、一見、奇妙なことである。論理は感覚や感情を排除しきったものであるはずだ。「論理」は"実感"ではありえない。けれどもこの学団には、そういうことは通用しなかった。論理実証主義は実のところは論理実感主義だったのである。シュリックからヴィトゲンシュタインまで、カルナップからゲーデルまで、ケンブリッジ学派から分析哲学派まで、かれらは論理が実感できたのだ。そしてゲーデルは、このウィーン学団から分析哲学におよんだ精神の正真正銘の嫡子だったのである。
いったい論理を実感するとはどういうことか、おわかりか。そもそも論理をつくるというのは、命題や問題を摘出することにはじまっていく。「床屋の髭を剃るのは誰か」という命題があることからはじめて、その命題の意味する主張ではなく、その命題を成立させている論理的な手続きに関心を向ける。したがって論理学者の多くは思想の主張なんかにはまったく関心がなく、その主張を支える論理の真偽性だけに注目する。つまり思想ではなく、思想を支える論理が問題なのである。
ということはどういうことかというと、命題や問題の所在に立ち向かった論理学者や数学者たちは、その命題や問題の成立の手続きを分析することによって、命題や問題が消滅することに異様な情熱を傾けたということなのだ! 問題を議論することが問題の消滅につながったのである!
これをゲーデルにあてはめていうのなら、むろんゲーデルとて問題の所在には関心がある。しかし、ゲーデルがさらに関心をもったのは、問題の所在があきらかになることはその問題が消えうせるものだと考えたからだった。
こうして、ぼくはこの時代のこの学団のまことに奇怪な論理的芸当というものの本質を、次のように言いたいとおもうのである。つまりゲーデルたちは問題を検証することによって新たな思想を打ち立てるのではなく、問題の消滅をこそおもしろがったのだ、というふうに。
そうなのだ、ウィーン学団や分析哲学派の連中と同様に、ゲーデルは、思想や哲学そのものではなくて、問題を解消していく「方法」だけを残したかったということなのである。さきほどのべたゲーデルの一つの確信とは、この「方法」のことである。「方法」だけにかかわる思考をして、方法以外の主張から自由になりたかったということなのである。ゲーデルの定理はここに出所した。
1938年、ウィーン学団はナチスによるオーストリア併合とともに消滅する。ウィーン学団のメンバーはほぼ全員が社会民主党の支持者であったのだが、それも学団が非合法とされた原因になった。
当時のナチスを甘く見てはいけない。ナチスは筋金入りの実用科学集団でもあった。このことはウィーン学団との決定的対立をあらわしている。ウィーン学団が統一科学の論理十字軍であるのなら、ナチスもまたアーリア民族のための世界科学十字軍だったのだ。その劇的な対決が1936年にモーリッツ・シュリックがウィーン大学の階段で射殺されるという事件にあらわれる。シュリックは、そのころ日の出の勢いをもっていたアインシュタインらとともに「ユダヤ的である」と判断されたのだ。
こうしてゲーデルはオーストリアを離れることになる。すでにアインシュタインもノイマンもメンガーもアメリカに移っていた。1940年、ゲーデルはニュージャージー州のプリンストン高等研究所に入る。
アメリカにおけるゲーデルを追うことは、実は不完全性定理を提唱したゲーデルを語るよりもずっとおもしろい。なにしろここにはアインシュタインがいたのだし、フォン・ノイマンもヘルマン・ワイルもオッペンハイマーもいた。
しかし、今夜はそのことを語るおもしろさを支えるぼくの"方法"がもたなくなっている。さっきから眠くて眠くてしょうがないからだ。
ゲーデルがその後に、アインシュタインと最も濃密な親交を結んで相対性理論から回転宇宙論を導き出したこと、ライプニッツの存在学とフッサールの現象学の研究に打ちこんだこと、その流れかどうかはわからないのだが、晩年にはプラトン主義とオカルティズムにどんどん片寄っていったことを付言して、床屋のパラドクスにはじまった今夜の話をひとまず閉じたいとおもう。
実はゲーデルは眠くなると、すぐにすべてを打ち切る趣味の持ち主だったのだ。