サルバドール・ダリ（１２１夜）のシュールな絵を教科書の端っこに見いだしたとき何を感じたか、アンデルセン（５８夜）の童話で泣いたのは何のお話だったのか、ジョン・コルトレーンの《至上の愛》をいつ聴いたのか、どんなときにジャン・ロレンツォ・ベルニーニ（１０３４夜）の彫刻《法悦》に息を吞んだのか、土方巽（９７６夜)の舞踏をどこで観たのか。
人生のセンスはだいたいこれで決まる。もうひとつ、ある。これらのことを誰と語りあったのかということだ。
１５歳のとき、担任で数学を教えていた赤井先生がやおら「メビウスの輪」を黒板に描いて、どうや、不思議やろ、表と裏がぐるっとつながっとるんやと言った。ノートを切ってねじった輪っかをつくって、何度も指で辿って不思議に溺れた。それからしばらくたって、桂寿一先生（デカルトの翻訳者）からエルンスト・ヘッケルの洋書『自然の芸術的形態』をもらった。１週間ずうっとページを繰っていた。
２０代のおわり、ダーシー・トムソンの『生物のかたち』（東京大学出版会ＵＰ選書）に出会った。並木橋の杉浦康平スタジオで、奈良原一高さんや武満徹さんを交えて、「かたちの美」はどうして仕上がっていくのかを夜遅くまで話した。
十川治江に薦められてバートランド・ラッセルの『神秘主義と論理』（世界思潮研究会）を読んだのはいつだったか。「数学は冷酷で厳粛な美しさである」とあった。
厳粛な美だけではなく冷酷な美でもありたいというところが、パラドックス好きで皮肉が相手に刺さるとエビぞって悦ぶラッセルらしかった。昭和初期に出回った「ラッセル叢書」第一編の古本だ（最近はみすず書房でも翻訳刊行）。
ラッセルの本を薦めた十川は数学の才能が長けていた女子で、知人を介して「遊」を手伝いたいと言って、創刊号を準備していた池袋の木造事務所棟の２階の一室にあった工作舎にやってきた。建築科の出身なので版下制作を手伝ってもらったのだが（東芝に就職していた）、彼女を紹介した知人の話では早稲田の理工をトップで卒業していたらしく、矢野健太郎が「これが３時間で解けたら天才」といってベストセラーの中に掲げた難問を15分くらいでスイスイと解く。のちにフィールズ賞の広中平祐が「おたくの十川さんの数学センスは抜群だね」と言っていた。
その十川と、ラッセルとホワイトヘッド（９９５夜）の共著『プリンキピア・マテマティカ』（岩波文庫）の序論を競って読んだのが、いまは懐かしい。十年ほど、彼女と何かにつけての数学談義を交わせたのは僥倖だった。
ぼくが工作舎を去ったのちの十川は、「ライプニッツ選集」の翻訳刊行にとりくみ（第1期全10巻・第2期全3巻）、たくさんの翻訳者たちを別にすると、その全容と細部のコントロールをキュリー夫人のごとくにほぼ一人でやってのけた。この選集は、ぼくにそもそもの数学的哲学のイロハを教えてくれた下村寅太郎さんの肝煎りだった。
左写真は1981年に、「遊」編集時代の工作舎スタッフが、来日した絵本作家レオ・レオーニと打ち合わせをしている風景。中央に十川治江さんが写っている。右写真は「遊」（特集：祭る、1981年）の「遊人紹介」に載った写真。プロフィールには「念願のライプニッツ翻訳も動き始めた」とある。
翻訳家でフォーラム・インターナショナル主宰の木幡和枝さんのお別れ会で、Plan-Bに松岡と工作舎メンバーが集結したときの写真（2019年）。一番右側に十川さん。その手前に工作舎社長の田辺澄江さん、左端に編工研の木村久美子。みな、かつて松岡とともに「遊」の編集に打ち込んでいた仲間たちだ。
数学を美的に感じる数学者はかなり多い。オイラーもポアンカレ（１８夜）も、高木貞治（５４夜）も岡潔（９４７夜）も、数学的な美学の極みに惚れぬいた。けれども、数学は美しくなければならないとか、数学はエレガントであるというような玄人好みの話は、たいていペダンティックな自慢話になりかねず、その感興は伝わりにくい。それを納得させるには、自分で数学に溺れるか、さもなければオスカー・ベッカー（７４８夜）ほどの独特な美学的な表現解説力がいる。
とはいえベッカーのように、鉛筆の先が尖って折れやすいようなフラジリティをもって数学美を解説できるというのはかなり特別な才能で、そうとうに言葉の美学にも通じていなければならず、そのため「美」はともかく、数学が苦手な者たちはせめて「数学的おもしろさ」には馴染んでおきたいというふうになる。それはそうだろう。数学というもの、不得意な相手ではあっても、邪険にするにはかっこよくて、セクシャルすぎるのである。だから、少しは付きあいたい。
では、どうしたら馴染めるのか。お近づきになれるのか。おそらく答えはただひとつだ。それはこういうものだ、「パターンに遊べるかどうかだよ」。
本書は、数学的思考や科学的思考におけるパターンの意味と効力を説明するにはうってつけだ。著者はアメリカではセントメリーズ大学の名物理学部長としてそこそこ知られてきたが、むしろイギリスでのサイエンティフィック・エッセイストとしてのほうが有名だ。
中身は「数学はパターンの科学である」ということをさまざまな角度から案内したもので、興味深い例が次々に繰り出される。図版も多い。全部につきあっているとやや“数学疲れ”が出てくるかもしれないが、それでも一般読者に読ませる技量には事欠かない。とくにデザイナーは必ず手元に置いておきたい。
構成は数学入門コースウェアとしてもわかりやすい。１「計算」（数、記号、ギリシア数学、素数のパターン、フェルマーの最終定理）から始まって、２「推論と伝達」（ブールの論理学、命題論理、述語論理、集合論、ヒルベルトとゲーデル、言語のパターン）、３「動きと変化」（無限級数、関数、変化率の計算、微分・積分、複素数、解析的数論）と進み、ここで４「形」（ユークリッド幾何学、座標、非ユークリッド幾何学、射影幾何学、次元）、５「対称性と規則性」（対称性の群、ガロア、壁紙のパターン、タイル張り）という日常感覚と非日常感覚をつなぐ幾何学を深めながら、いったん６「位置」という見方のおもしろさ（オイラーの定理、ネットワーク、トポロジー、多様体、結び目）を展開して、最後にまたフェルマーの定理に戻っていく。
こういうみごとな構成で、おまけに１章ごと１節ごとの展開スピードが心地よいので、その味に酔える。
キース・デブリンは、1947年キングストン生まれ。熱心な数学啓蒙活動を行う一方で政府関連機関のコンサルティングなど多彩なキャリアの持ち主。現在はスタンフォード大学言語情報研究センターの研究者をつとめている。図版は『数学：パターンの科学』の原著で、表紙絵はカンディンスキーの《イン・ブルー》である。「青が深まるごと、なおいっそう人間に無限への思慮を呼び起こし、純粋さや、ついには超感覚的なものへの憧憬を喚起する」（カンディンスキー）。
『数学：パターンの科学』の図版ページ①
「第2章 推論と伝達」p.94‐95
『数学：パターンの科学』の図版ページ②
「第3章 動きと変化」p.152‐153
『数学：パターンの科学』の図版ページ③
「第4章 形」p.182‐183
『数学：パターンの科学』の図版ページ④
「第5章 対称性と規則性」p.260‐261
『数学：パターンの科学』の図版ページ⑤
「第6章 位置」p.292‐293
たとえば第２章「推論と伝達」は、カントールの集合論の意味を説明しながらラッセルのパラドックスを紹介し、そこからヒルベルトの問題の立て方とゲーデルの定理を両睨みすると、ポール・コーエンの画期的な方法を挙げ、ついでチューリング・マシンの意図を解き、さっと「言語にもパターンがある」という話題に突っ込んでいく。
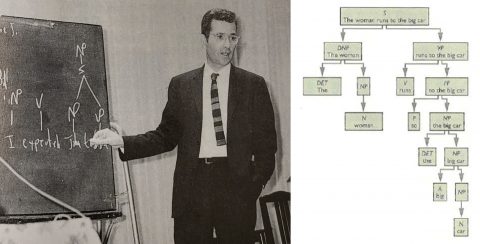
この「言語にもパターンがある」についての説明では、ソシュール、ボアズ、ブルームフィールドが横並びに紹介され、そのあとただちにカルナップの論理実証主義とチョムスキー（７３８夜・１８１８夜）の生成文法論が解説される。この手際がなかなか適確で、かつ早くて気持ちいい。
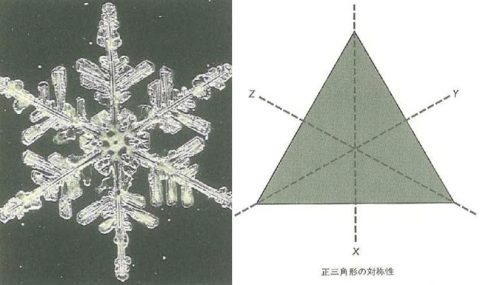
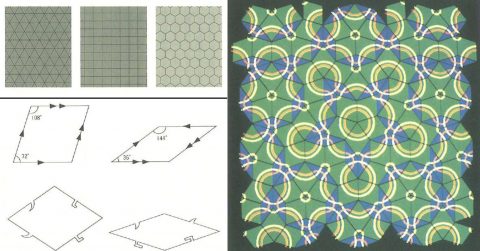
第５章「対称性と規則性」では雪の結晶から入って、パターンはしばしば「対称性の群」によって変換されるという図形変換的な話に進み、代数のような抽象的な数学でも対称性や変換性がおこりうること、この問題に立ち向かった若き天才ガロア（２０才で決闘死）の話とそこから発展した「群論」の概要を案内したうえで、これらをフェリックス・クラインが「エルランゲン・プログラム」（1872）として幾何学の統合的な展望に仕向けていったこと、そこから射影幾何学やトポロジー（位相幾何学）という新分野が誕生していったことなどにふれる。
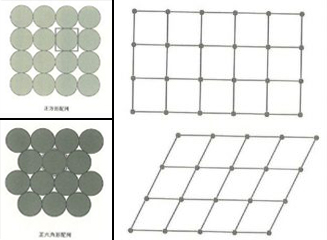
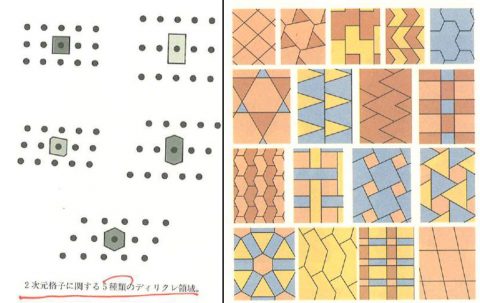
この章では「詰め込み」と「積み上げ」の話がとびきりおもしろい。リンゴやミカンをどのように詰め込むと一番効果的なのかといった例は、ガウスの「格子状詰め込み問題」の解法に始まり、これがラグランジュの数論にまで発展するのだが、一方ではこの手のパターン数学が鉱物の結晶問題、ダーシー・トムソンが着手した生物の形態進化とパターンの関係の謎、壁紙やタイル張りの妙、ウィリアム・モリスのレッサーアーツ、ディリクレ領域（Dirichlet allocation）やボロノイ図のもつ意味、ロジャー・ペンローズ（４夜）の周期性と非周期性の研究（）準結晶の研究）などにも及んでいることを案内する。いずれも鮮やかな事例だ。
とくに本章に登場するジョン・ホートン・コンウェイがボール紙で示した「空間の非周期的なタイル張りの二重プリズム模型」（1993）は、見ているだけで興奮する。この数論と立体モデルで図抜けた才能を発揮したお洒落な数学者コンウェイは、さきごろのコロナに罹って亡くなった。
ちなみに本書はフェルマーの定理を何度も引いて議論をすすめているが、そのあたりのことはサイモン・シン（４３５夜）の『フェルマーの最終定理』の千夜千冊でやや詳しくふれたので、そちらを読んでもらいたい。
左図の雪の結晶は、中心を軸として60度回しても元の形と不変となる対称性をもつ。右図の正三角形には、恒等変換、2種類の回転、3本の軸の反射（線対称移動）による計6個の対称性を保つ変換があり、どの変換を組み合わせても同じ形が保たれるので、これらを正三角形の対称性の群という。この「群」という概念の原型はガロアによるもので、五次方程式が根号でとける条件は、解の持つ数学的な対称性によって決まるという発見にもとづく。
『数学：パターンの科学』「第5章 対称性と規則性」p.233‐238
球を詰め込むときに、正方形配列（左上図）と正六角形配列（左下図）の二種類の内、どちらが効率的か。ガウスは、1831年に、右図のような「格子」（＝規則的な二次元的な編み目の頂点に並んだ点の集まり）という概念を想定した場合において、正六角形配列が最も効率がよいと導き出した。
左図は2次元格子に関する5種類のディリクレ領域。ディリクレ領域とは、他の格子点からの距離よりもこの格子点からの距離のほうが近いような点の全体のこと。平面上に出現可能なディリクレ領域はこの5種類しかない。また壁紙のパターンも、対称性の群という意味では右図のとおり17種類しかない。
タイル張りは、周期的（平行移動に関する対称性）に平面を埋め尽くせる正多角形は何かという問題だ。左上図の正三角形、正方形、正六角形が単一の正多角形で埋め尽くせるパターンで、複数の正多角形による組み合わせは8通りある。ロジャー・ペンローズは、非周期的で平面全体を埋め尽くせる左下図のような図形の組み合わせを発見した。右図の平面全体のペンローズのタイル張りの一部分をみると、明らかに局所的な五重の対称性が見える。この構造は、結晶学者が準結晶を発見することにより重要性が増した。
1993年にジョン・コンウェイが発見した二重プリズムのボール紙による模型で、空間の非周期的なタイル張りの一部分を示している。二個の傾斜した三角プリズムを組み合わせることで、凸多面体で三次元空間を埋め尽くしている。
数学はどう転んでもパターンをどう使うかというしくみを中心にできている。数学はパターンの科学にすぎないと言ってもいい。パターンを無視した数学があればお目にかかりたいほどだ。
ただし本書はパターンという用語ですべてをすませているが、パターンにもいろいろがある。フォーム、フォーマット、テンプレート、スタイル、モールド、モデルなどもパターンに入るし、日本では「形」も「型」も「体」も、「風儀」「形式」「形態」も、「紋切り型」も「鯛焼き」も「鯛焼きのための鉄板」も、みんなパターンなのである。洋裁でパターンといえば型紙のことだし、エソロジー（動物行動学）でパターンといえば、繰り返しあらわれる動きのことだ。心理学では「ゲシュタルト」が知覚とともにあらわれるパターンのことだった。クリストファー・アレグザンダー（１５５５夜）は、建築設計にもパターン・ランゲージがあると言った。
こういうぐあいにパターンと言ってもいろいろなので、パターンとは何かということ自体を目くじら立てて追求しないほうがいいかもしれない。そこにパターン的なものが認められれば、すべてパターンなのである。パターンがどういうものかということより、どんなパターンであってもパターンをつかって思考や制作をすすめ、それが「世界を見るための方法」を示している、その方法が数学から読みとれるということが、とりあえずは重要なのだ。
なぜ文明が「数」をもったのかということは、人類学にとっても数学にとっても面倒なほどの大問題で、あまり説得力のある説明がなかったのだが、「パターンの発生」という視点からみれば、それほどの難問ではない。
そもそも「数える」ということは、与えられた集まりに含まれる「メンバーの個数というパターン」を知ることなのである。それゆえ、そこで使われる数字という記号はパターンのためのトークン（代用品）からの転用だった。
スリランカのベッダ族はココナツの個数を数えるのに木片を用意して、ココナツ一つずつに木片を対応づける。全部でどのくらいココナツがあったかというときは、木片の山のほうを見る。そして「たくさんある」と答える。ここでは木片が数字の代わりのトークンだ。このトークンと数字とのあいだのどこかに「思考をはこぶパターン」が出入りした。
幼児には、目の前の立体物が面や線でできていることはどうしてもわからない。体積という概念もわからない。そこでジャン・ピアジェ(１８１７夜)は、幼児が立体や体積を理解するには、少し年齢がすすんでパターンというものを学習しないかぎりはいつまでも理解は得られないと強調した。子供にはなるべく早く「パターンで見ること」を教えるのがいい。そのうえで自由な発想に向かったほうがいいとも強調した。
つまりパターンには、これを動かそうとしたり、何かにあてはめようとしたりすると、「思考に何かをもたらすパターン」のせめぎあいがするすると寄り添ってくるわけで、数学を愉しむには、この寄り添ってくる「思考の型」とどんなふうに親しむかがキモになる。
これはぼくが編集学校でまず「型」を教え、ついでその「型」を使って何かを表現することを遊んでもらい、最後に世界観の中にいかに多くの「型」が組み合わさっているかを学んでもらっている手順と同じだ。子供も大人も何を学習しているのかといえば、「世界をパターンで見る見方がいくつもある」ということに勇気をもって乗っかれるかどうかなのである。
この手続きをわかりやすく手順で解くのが数学だ。数学は立体物や時空間についてさえ、他のいくつかの物体によるパターンの組み合わせによって理解する。
ロシアの飛び地カーニングラードが、プロイセンのケーニヒスブルグと呼ばれていたころ、郵便配達人は一つの問題を抱えていた。それは、図のような7つの橋を重複せずに渡れるかどうかというものだった。この「一筆書き問題」を不可能だと証明したのがレオンハルト・オイラーだった。頂点につながる辺の数は全て偶数か、奇数の頂点が2つでなければならないからだ。その後、このような点と線の関係を考察する分野として「グラフ理論」が発達し、地下鉄の路線図や電気回路図になっていく。
世界の見方の一つにトポロジー（位相幾何学）がある。ひっくり返したり拡大や縮小を繰り返したりしても保存される図形の性質を取り扱う学問である。19世紀に定式化された四色予想問題もその一つである。図のように、同じ色が接することなく地図を塗り分けるには最低四色あれば可能だという予想は、20世紀にコンピューターを使って、600以上の場合分けを網羅的に行って証明された。
というわけで、「数」にまつわるもともとの由来をいえば、１つとか３本とか４７個と数えているというそのことが、「世界をパターンで見る」という数え方の発生（つまりは「数」の発生）だった。数えるという行為そのものが自然数をパターンで表現したということだった。
それならわれわれが「１つ、３本、４７個」と数えられるようになれたのは、どうしてかといえば、ひとつには指を折ってみること（ディジットすること）を知恵として自覚できたからだろうが、これだけでは数を運用できなかった。指を折ってみるだけでは数えた記憶がのこらない。そこで数の記録を何かで示しておくことにした。こうしてトークンが介在することになった。
トークンなら日にちがたっても数がのこる。このエビデンスについては70年代後半から80年代にかけて、人類学者のデニス・シュマント＝ベッセラートが古代イランのスーサの出土品から調べ上げた。粘土製のトークンに数のぶんだけの線分や穴が刻まれていた。
かくてトークンが先行して、ここから記号や数字が派生したわけである。そこからは各地で計数システムがさまざまに工夫され、指折りでは賄いきれない「桁上がり」も思いついた。
数学の原型は、このような「トークンとしての数学」と「学習されたパターン」とをたくみに組み合わせてできあがっている。もう少し正確にいえば、数学的な思考がパターンによっているということは、数学はパターンによって「数による計算」という抽象的な思考を維持しているということだ。そのことによって推論に沿った抽象的な構造も想定できていったということだ。「数えられる数」はのちに自然数と呼ばれた。
シュメール人は社会構造の複雑化に伴い、トークンの形状をより精巧なものにした。左上の写真は（上段左から右へ）1頭の羊、1単位の特殊な油、1単位の金属、1様式の衣料品、（下段）別様式の衣料品、未知の生活必需品、1容量のハチミツをあらわす。官僚制度が発達すると、トークンを容器に入れて保存するようになった。左下の写真は、球型の容器（エンベロープ）と中に密閉されていたトークン。中を開かずとも数量が把握できるように、容器表面にはトークンを押し付けた刻印を施した。すべて紀元前3300年頃のもの。右の写真も同じくシュメール人が穀物の数量を記録した粘土板。物理的なトークンは姿を消し、板状の「しるし」へ成り代わっている。紀元前3100年頃のもの。
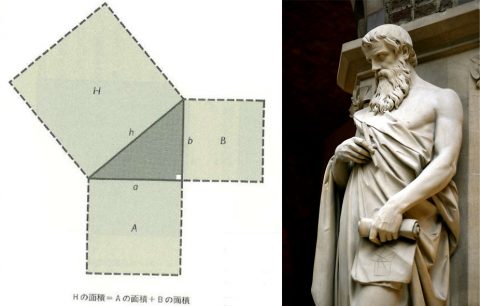
旅商人であったミレトスのタレスは、「円はその直径によって二等分される」とか、また「相似な三角形の対応する辺は比例する」という洞察をした。これはまさに抽象的な構造を視覚的に明示したもので、そこからピタゴラスのクロトン学派が登場し、次の時代の幾何学と抽象数学の第一歩を踏み出した。
ピタゴラスの提案は、知というものは「数と音と図」の組み合わせであるということだった。だからピタゴラスはクロトンの学園に、①アリスメティカ（数論）、②ハルモニア（音楽）、③ゲオメトリア（幾何）、④アストロロギア（天文）という４科目を掲げた。それを「クアドリウィウム」（４科）といい、のちに中世ラテン世界でこれに論理学・文法・修辞学の「トリウィウム」（３科）が加わって、これらがのちのヨーロッパの７つの「学芸」になり、やがてが自由七科としての「リベラル・アーツ」になった。ヨーロッパの知は最初の最初から「パターンの組み立て」に発していたわけである。
このうちのゲオメトリアをユークリッドが発展させた。ユークリッドは『原論』に定義と公理から２２個の定理を案出し、そのうえで５つの公準を提示した。「任意の点から任意の点に直線を引くことができる」とか、「任意の中心と半径をもつ円を描くことができる」といったものだ。公準はのちにヒルベルトによって２０個にふえたけれど、いまなお幾何学の基礎になっている。
ここに「形、平面、角度、長さ、高さ、面積、比、同じ、違い、移動、内側と外部、大小」といった認知の要素が、数学的に掴み出せることになった。これらはいまではすっかり幾何学の基本文法のような顔をしているが、その出自からして「パターンをつかって対象を解釈するための認知道具」だったのである。
ユークリッドは『原論』第7巻に、偶数と奇数のちがい、素数の性質、算術の基本法などについても書いた。そこには、のちにモジュラス（有限算術）として扱われる考え方が先取りされていた。それを近代数学の意匠に仕上げたのは若きカール・フリードリッヒ・ガウスである。ユークリッドとガウスによって、パターン思考が幾何から代数に移行できるようになった。パターンは、数学が乗り換え、着替え、持ち替えをしながら、代数やら幾何やら解析やら応用数学やらと様式を選択していくにも絶必だったのである。
「ピタゴラスの定理」といえば、直角三角形の斜辺の上に描いた正方形の面積が、他の二辺の上に描いた正方形の面積の和に等しいことを主張するものだ。著者はこの業績で驚くべきは、任意の直角三角形において成立することを厳密に証明したことにあると指摘する。図はユークリッド（右写真）が定理の証明に用いたもので、三角形の各辺上に描いた正方形を活用する。
左写真はユークリッド『原論』の最古の写本の断片（BC100年）。右図は『原論』の1ページ。パターンをつかって対象を解釈するための「認知道具」が並ぶ。
1801年に弱冠二十四歳のガウスが発表した『数論研究』の写本。「有限算術」のアイデアが展開され、後に「数論」が一つのジャンルとして確立される端緒となった。有限算術はプリミティブな操作で行われる。数が周期的に元に戻るような数え方で、代表的なものでは「時計の算術」が当てはまる。例えば、時計の短針は2時から3時間進めば5時、11時間進めば1時を指す。
2+3=5, 2+11=1
足し算として奇妙な感じを受けるだろうが、通常の算術から有限算術へと、数学的なパターンとしての「算術的構造」をまたいでいる証である。
数学には命題と証明がつきものだ。命題が与えられ、これを順々に証明していくプロセスは数学の独壇場である。しかしながら、そこに次から次へと数式が登場してくるのは、数学の苦手な者には食後のたびに2錠のめばすむ風邪薬にくっついている長々しい使用説明のようで、できれば御勘弁ねがいたいところだろう。
けれども、これは数学が真偽のいきさつを雄弁に組み立てるべく、主語と述語をいろいろ持ち出しているプロセスであって、いわば小説の描写のようなものなのだ。この数式の展開がなければ、数学は文明の一切の記述から抜け落ちていく。
数学の証明につきあうのは風邪薬の説明を読むよりうんとエキサイティングで、どちらかといえばスマートな推理小説の展開に近い。ただし、ここで探されている主語や述語は、小説の叙述とは異なって、ひとえに「論理」（あるいはその代用品）というものなので、証明プロセスにおける数式の展開では、パターンはいろいろ組み合わさって論理の姿をとることにした。
そういうふうにしてみようと最初に思いついたのは、他の多くのお題設定がそうだったように、アリストテレス（２９１夜）だ。アリストテレスは三段論法などの考案でも知られているが、パターンの組み合わせの進行を「主語述語命題」という論理の見え方に移行させた。これによって数学は、主語と述語にもとづく論理の行方をあらわせるようになっていく。論理の行方をあらわすとは「推論」のプロセスを示すということである。
ところがアリストテレスが着手した推論の手続き（論理的推論）は、その後はあまり発展しなかった。やっと19世紀半ばになってジョージ・ブールが登場し、思考のパターンを代数的に把握しようと試みて、ようやく論理を代数化することができるようになった。主語述語命題は（代表的にはあいかわらずの三段論法）、ブールの代数論理学（ブール代数）によって新たな様相を獲得する。
ブール代数はのちのコンピュータのもととなり、アルゴリズムとしてのプログラムをつくるうえでの大前提になっていく。
アリストテレスは命題には全4種類（上図）あると考え、この4種類の命題を、大前提、小前提、結論の三つとして組み合わせる三段論法によって、機械的に推論を運ぶことができると考えた。下図は三段論法の一例。
ブールは命題をなにかの集まりについて記述したものと見立て、その記述を算術記号に置き換えることを試みた。図はその証明例である。代数的操作により、読み解きやすい論理構造に置き換えられたため、アリストテレスの論理学に一部矛盾する点があったことがのちに判明した。
こうして数学は、論理もまたパターンであると確信するに至ったのである。真偽もパターン・フォーメーションの精査によって証明できることになったのだ。
しかし、数学的な真偽を証明するプロセスにどのようなパターンが出てくるかということは、新たに「論理パターン」とでもいうべきものを想定するしかない。論理パターンは数や三角形ではない。何が何して何とやらという考えの進め方をパターンにすることだ。
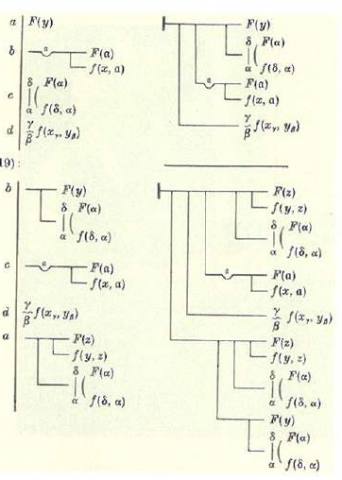
そんな論理パターンで数学的思考をあらわすには、どうしたらいいのか。ジョゼッペ・ペアノやゴットロープ・フレーゲの出番がやってきた。ここでちょっと告白すると、ぼくが数学を邪険にするまいと決めたのは、フレーゲの概念記法と述語論理の扱いに出会ってからのことだった。
ペアノは寡黙だったようだが、多才である。自然数の公理系の確立者で（ペアノの公理）、存在記号や包含記号の考案者、また無活用ラテン語の発案者としても知られている。が、なんといってもペアノ曲線の発見者としてピカピカの数学星座として輝いた（ペアノの図形）。
これは閉じた平面（空間）を単位正方形に分割したとき、どのくらい連続的で空間充填的な図形が埋め尽くせるかという問題に挑戦したもので、パターンの魔術の特例のように19世紀末の数学界の話題になった。いっとき十川がはまっていた。ある日、「やっぱりペアノですよ」と言い出したのだ。十川の資質はこういう目にも綾なる数学に惚れるところにあったようである。十川にとっては、これがベルニーニでコルトレーンだったのだろう。
ペアノの図形論からは、その後シェルピンスキーのガスケット図形、コッホの雪片曲線、マンデルブロのフラクタル図形などの姉妹たちが生まれ、なかでもブルーノ・ムナーリ（１２８６夜）がシェルピンスキーの閉じたペアノ曲線に惚れて、これをいろいろなデザインに転用したことでも有名になった。もっとも論理パターンの数学としては美しすぎて、十川は憤然とするだろうけれど、おそらく数学思想史からは敬遠されたのだと思う。
数学において曲線とは、直線でない全ての線をいう。分割された正方形を一筆書きできる線をペアノ曲線と呼ぶ。図の様な正方形だけでも272通りの曲線がある。
図は4つずつに分割する方法で作図されたヒルベルト曲線。分割を無限に繰り返すと、このような曲線は平面すべてを埋め尽くすため、「空間充填曲線」とも呼ばれる。
左上のシェルビンスキーのギャスケット図は、正三角形の辺の中点を結び、新しい正三角形を作る操作の繰り返しでできる。右上のコッホ雪片は、コッホ曲線を三角形の各辺にしたもの。コッホ曲線とは、線分を三等分し、中央が正三角形の２辺になるような線分である。左下のマンデルブロ集合は, 歴史上初めてフラクタル図形として定式化された複素数の集合。これらのフラクタル図形の特徴として、無限に操作を繰り返す限り、曲線の長さは無限になる。右下は、ブルーノ・ムナーリがペアノ曲線を利用してデザインしたグラフィックデザイン。
一方、フレーゲの「概念記法」（Begriffsschrift）は、まったく新しい「数理論理学」をつくりあげた。論理のはこびを特別な論理操作記号で記述して、それを述語論理として計算できるようにしたのだから、これは腰が抜けそうな変革の狼煙だった。１８７９年の狼煙である。
論理操作記号による計算は哲学史上、数学史上、言語史上のいずれにおいても初めてのことで、パターン性の高い略式言語の可能性を告げた。述語論理はアリストテレスの命題論理をいわば文章（フォーミュラと呼ばれる）に拡張したもので、哲学が代数になりうることを宣言した。いずれも前代未聞、フレーゲはいつのまにこんなことを考えていたのか、何をどう工面してこんなアイディアを「論理パターン」で動かせると思ったのか、その秘密を知りたくなったものだ。
おそらくフレーゲは「入れ子型の思考」とはどういうものかということを考え抜いて、そこで覆われがちになる構造を隠さず明示化できるような方法はないものか、そこをつくろうとしたのである。非可述的（impredicative）な二階量化や多重量化（multiple quantification）がこうして誕生した。
フレーゲによって数学の論理的進行は、あっというまに、「かつ」「または」「～でない」「～ならば」と、および「すべての」と「いくつかの」の数量詞程度で、ほぼあらわせるようになった。まさに「計算できるパターン・ランゲージ」が数学界の手に入ったわけである。
フレーゲは、量化や関数など独特の考え方をレゴブロックのように組み合わせることによって、どのような概念の流れも表現できる一般的な概念の記法を確立しようと考えた。図は量化、関数、関数の操作に関する記法。
フレーゲは概念記法を組み合わせることによって「関数を量化する」入れ子構造の表現まで考えた。図は『概念記法』に書かれた式。y=2xなどのなじみある方程式で右辺と左辺に操作を加えるのと同じように、関数同士を計算する式変形が連打されている。
それならフレーゲの概念記法のおかげで数学がすっかり記述的な変貌をとげたのかというと、そうではなかった。つまりダンテ（９１３夜）やシェイクスピア（６００夜）によって文学が様相を変えたように数学も変貌していったのかというと、そうではない。
数学は「意味の科学」ではなく、あくまで「パターンの科学」だったので、とくに当時は、ここから言語に代わる数学言語によって思考を自由に操れる方法は生まれてはこなかったのだ。それをおこすには、ヒルベルトの超数学の登場と、ゲーデルの反論と、そしてアラン・チューリングの万能計算マシンのアイディアが連打される必要があった。
とはいえ、これらの連打からむくむくと形をなしていった20世紀後半のコンピュータの驚異的出現が、言語的思考のプロセスを数学思考に置き換えていくようにしたかといえば、それはそうでもなかったのである。また、数学本来の行く末も、そのことを念願していたわけでもなかった。
では念願の「パターンの科学」を言語や意味にまで及ばせるというフレーゲ発進の道筋はその後どうなったかというと、ここからは「システムとしての言語学」に研究の先端が軌道転換していって、ソシュール、ボアズ、ブルームフィールドらの共時的言語学や、ヴィトゲンシュタイン（８３３夜）、カルナップ、ハリスらの論理実証主義や、チョムスキーの生成文法論、および記号論理学のほうへと課題が転じていってしまったのだった。
うっかり「パターンの数学」では言語の秘密が解けなかったという話にしてしまったが、これはないものねだりだったかもしれない。デジタル・コンピュータがこんなに世の中にいきわたったのだから、ブール代数やフレーゲ論理算術の本懐は存分に遂げられたということだろう。
1966年に来日した際、生成文法論について講演するチョムスキー。英語の文法規則として７つほどの「パターン」を示し、英語の文構造をパース・ツリーとして表現した。言語の抽象的構造を具体的に把握するというこの方法が、コンピュータ言語のパーサ（構文解析器）として活かされていく。
数学史における「パターンの数学」には、実にいろいろなものがある。パターンそのものの種類をふやしてもいったし、パターンを置いておく台座も用意されたし、パターンが変化していく推移を追った数学も試みられた。
デカルトのXY座標系は台座である。古代以来の立方体の倍積問題や角の三等分問題も、ガウス、ロバチェフスキー、ボヤイ、リーマンが取り組んだ非ユークリッド幾何学も、ルネサンス絵画に採り込まれた遠近法も、17世紀に証明されたデザルグの定理も、n次元空間がありうるということも、台座がなければ生まれなかった。
対称性がもたらす「パターンの数学」はかなり豊富だ。そもそも合同とか相似という見方が獲得できたのもパターンの動向を対称性から得たものだった。対称性がもつ意味については、ヘルマン・ワイル（６７０夜）やマーティン・ガードナー（８３夜）の千夜千冊でも紹介しておいた。先に述べたペンローズやコンウェイのことも忘れないでほしい。
パターンに光と位置をもたせると新しい数学が生まれうることは、射影幾何学とトポロジーが鮮やかに見せつけた。ぼくは杉浦康平が「数学セミナー」の表紙デザインをしていたときに杉浦さんと仕事をしていたのだが、当時の杉浦さんが位相幾何学とトポロジーをさまざまなデザインに応用しているのを見て、ずいぶん刺激をうけた。それに奈良原一高さんや武満徹さんが加わって、先にも書いたが、ある一夜をメビウスの輪やクラインの壺を音楽や写真にするにはどうしたらいいかという話題で過ごしたものだ。
そのときぼくはポアンカレの代数トポロジーとリスティングの結び目の話を持ち出してみたのだが、音楽談義に色気を添えるほどにはならなかった。それからというものである、ぼくが数学と音楽を愉しむ夜こそ最もダンディでなければならないと思うようになったのは。
70年代に杉浦康平さんが手掛けた「数学セミナー」の表紙。トポロジー、群論、複素関数、確率論、カオス、フラクタルなど、現代数学のテーマに合わせた幾何学パターンと、短い数学コラムを一緒にレイアウトし、当時としては画期的な「読む表紙」、「考える表紙」になっている。
TOPページデザイン：美柑和俊
図版構成：寺平賢司・梅澤光由・大泉健太郎
桑田惇平・齊藤彬人・中尾行宏・上杉公志
⊕『数学:パターンの科学 ― 宇宙・生命・心の秩序の探求』⊕
∈ 著者：キース・デブリン
∈ 訳者：山下純一
∈ 編集：松田春樹
∈ 協力：日本経済新聞社科学出版部
∈ 発行者：小林豊彦
∈ 発行所：日経サイエンス社
∈ 印刷：奥村印刷
∈ 製本：積信堂
∈ 発行：1995年
⊕ 目次情報 ⊕
∈∈ はじめに
∈∈ 数学とは何か？
∈ １ 計算
∈∈ 数の起源
∈∈ パターンと記号
∈∈ ギリシャ数学
∈∈ 素数
∈∈ 有限算術
∈∈ 素数のパターン
∈∈ フェルマーの最終定理
∈ ２ 推論と伝達
∈∈ ギリシャの論理学
∈∈ ブールの論理学
∈∈ 命題論理
∈∈ 述語論理と言語のパターン
∈∈ 抽象化と公理的方法
∈∈ 集合論
∈∈ ヒルベルトのプログラムとゲーデルの定理
∈∈ 論理学の黄金時代
∈∈ 言語のパターン
∈ ３ 動きと変化
∈∈ 運動のパラドックス
∈∈ 無限級数
∈∈ 関数
∈∈ 変化率の計算
∈∈ 微分法
∈∈ 微分方程式
∈∈ 積分
∈∈ 実数
∈∈ 複素数
∈∈ 解析的数論
∈ ４ 形
∈∈ ユークリッドの公理
∈∈ ユークリッドの『原論』
∈∈ 座標幾何学
∈∈ 三つの古典的問題
∈∈ 非ユークリッド幾何学
∈∈ 射影幾何学
∈∈ 次元
∈ ５ 対称性と規則性
∈∈ 対称性の群れ
∈∈ エバリスト・ガロア
∈∈ 球の詰め込み
∈∈ 壁紙のパターン
∈∈ タイル張り
∈ ６ 位置
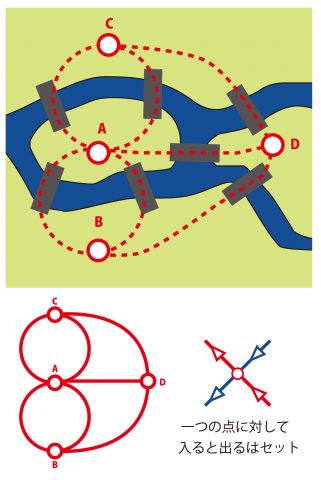
∈∈ ケーニヒスベルクの橋
∈∈ ネットワーク
∈∈ トポロジー
∈∈ 曲面の分類
∈∈ 多様体
∈∈ 結び目
∈∈ 再びフェルマーの最終定理
∈∈ おわりに
∈∈ さらに学びたい人のために
∈∈ 図版・写真出典一覧
∈∈ 訳者あとがき
∈∈ 索引
⊕ 著者略歴 ⊕
キース・デブリン（Keith Devlin）
1947年生まれの数学者。米国セントメリー大学理学部長。英国『ガーディアン』 紙に数学やコンピューターに関するコラムを執筆。BBCでテレビの数学番組の制作に携わったこともある。著書に『Mathematics: The New Golden Age』『Logic and Information』などがある。
⊕ 訳者略歴 ⊕
山下純一（やました・じゅんいち）
サイエンス・ライター。1948年生まれ。東京工業大学理学部数学科卒業。名古屋大学大学院博士課程満了。20世紀の数学史と物理学史に興味をもっている。『ガロアへのレクイエム』『ガロアの神話』『メビウスの遺産』（いずれも現代数学社）、『数学史物語』（東京図書）など、多数の著訳書がある。
