数学する身体

　能楽師の安田登さん（１１７６夜）から「数学を研究していて、ときどきぼくの会にやってくるおもしろい青年がいる」と聞いた。「松岡さんも会ってやってください、なかなか凄いですよ」とも言われた。そうこうしているうちに、その青年が森田くんで、その森田くんが文芸誌に身体的数学論を連載していて、それが本となり小林秀雄賞をとったことを知った。『数学する身体』である。
　読んでみて、気持ちがよかった。ヒルベルト（１３３夜）とゲーデル（１０５８夜）をめぐる一番大事な流れから、あたかも水を掬うように数学本来の考え方と接し方を適確に汲み上げている。数学が若水のように扱われていた。扱われている話題は特段に新しいことではないのだが、考えるセンスと書きっぷりが瑞々しい。とくにチューリングと岡潔を並べていったところは鮮やかだった。

物心ついてからバスケに夢中だった少年には、机上の数学は狭すぎた。大学は文系に進み、社会の枠にはまらない新たな実践を模索する。ある日、書店で岡潔の『日本のこころ』に出会い、数学もバスケも全身を挙げる行為なのだと感得し、数学科への転身を決めるほどにのめり込んでいった。
デビュー作にあたる本書は小林秀雄賞を最年少で受賞した。奇しくも半世紀前の新潮誌上では、岡潔と小林秀雄による対話『人間の建設』が連載されていた。

森田真生と安田登による講演会の様子。2017年9月22日に『能　650年続いた仕掛けとは』（新潮新書）の刊行記念イベントとして行われた。講演タイトルは「能を数学で、聞く」。考える人Web上にレポートが掲載されている。
https://kangaeruhito.jp/interview/1368

　この本は「数」をめぐる思索から始まって、だんだん数学の役割を解いていくというふうに進む。冒頭、存在の海に差異の亀裂が走って「私」と「世界」が立ち上がっていくなか、ヒトにおいては２と１が同時に到来したにもかかわらず、数学ではまず１があり、それに2が続いて”数直線”を措定していったのはどうしてなのかという疑問がむくむくとあらわれてくる。
　算盤のこと、筆算のこと、アラビア数学（アルジャブル）のこと、イタリア各地の計算学校やコスの技法のこと、デカルトの方法の工夫のこと、つまりは「算数ってどうしてできあがってきたのか」という話をあれこれ紹介したうえで、森田くんは自分が出会えた二人の哲人からの強烈なヒントを持ち出して、話を一気に若水掬いの手際にもっていく。
　一人はアンディ・クラーク（１７９０夜）で、主著『現れる現在』に「認知は身体と世界に漏れ出す」とあることを引きながら、数学も長らく「脳」や「心」に閉じ込められていたものが体に滲み出していったのではないかと確信するようになる。
　もう一人は荒川修作だ。荒川の養老天命反転地や三鷹天命反転住宅に衝撃を受けた森田くんは、数学もそのような「私と」「世界」を反転させる試みに向かっていったのではないかと思うようになる。実際にも三鷹の一室に住んでみたようだ。

図はレオナルド・ピサノ著『計算の書』掲載の「指で数える絵」写本。中世ヨーロッパには両手だけで9999まで数える手法があった。ポーズする手の上には数字の記載を確認できる。
数を媒介しない数量経験は漠然としている。一目見て、111本のマッチの正確な個数を認識することはできない。そこで”数”という道具を用い、様々な工夫をこらして、認知能力を延長してきた。その最たるものが身体の助けを借りる方法だった。

エジンバラ大学の哲学教授で、身体性認知科学の世界的リーダー。ハードテクノとレイヴをこよなく愛す。クラークは「心が脳だけにあるわけではない」と主張している。その証左として、薬で表情筋を硬直させると文章の理解が遅れる例や、自宅で日常生活をこなしていたアルツハイマー病の患者が、病院に入院した途端に自力で生活できなくなった例を挙げる。身体や外部環境で行っているループが、理解や認識に寄与して心の一部を作ると考えたのだ。

1963年、ニューヨークを拠点に活動していた30歳の荒川修作。身体感覚を再構築することで、新しい文明を開くことができる確信し、パートナーで詩人のマドリン・ギンズとともに体の感覚や常識を問い直す作品を発表し、「世界のアラカワ」と呼ばれる。生前まで「私は、死なないことに決めた」という名言（迷言）を言い続けていた。

《養老天命反転地》。荒川修作氏とそのパートナーで詩人のマドリン・ギンズの構想によって実現したテーマパーク。約18,000㎡に及ぶ広大な敷地に、傾いた建物や椅子など、人間の平衡感覚や遠近感を混乱させる仕掛けを設置されている。荒川が考えた「天命反転」という用語は、天から授かった命はやがて寿命を迎えるが“死なないため”に五感・本能を目覚めさせるという意味がある。来場客に身体のもつ様々な可能性を発見させることが狙いだが、開園当初はケガ人が続出したという。

　話はこのあと、デデキントやカントールが創成した集合論に致命的な欠陥があること、それを指摘した「ラッセルのパラドックス」に対してヒルベルトが救いの手をのべる超数学を提案して、数学についての議論を数学自身の議論にしたこと、しかしその数学は自身の無矛盾を証明できないとゲーデルが証明したという、例の一連の「超数学と不完全性定理のドラマ」を一瞥しながら、アラン・チューリングがこれらの議論に巻き込まれることなく算数の原理の<外部化>にとりくみ、万能計算機のモデルとしてのチューリング・マシンを提案したことを詳しく述べる。
　一応は詳しく述べるのだが、そうしておいて一転、後半を岡潔（９４７夜）の「情緒の数学」をめぐる話題に振り切っていくのである。天命反転だ。
　なぜ森田くんはチューリングと岡潔という真っ向対立しあうような数学思想を並べられたのか。かつ岡潔を絶賛できたのか。センスがいいとしか言いようがないけれど、そこにはなにがしかの背景があるはずだった。

　あとがきを読んで、ほうほう、そうかそうかと思った。「中学2年のときに甲野善紀の身体的知性に触れたことは幸運だった」と書いている。甲野さんはぼくもずいぶん昔から知っていた武術家で、工作舎にたびたびやってきてあたりかまわず真剣を抜きながら、ぼくのスタッフたちに体の動き方を説明していた。
　そういう甲野さんは、森田くんにとって身体を考えるときの師範で、また「独立した研究者」の模範であったらしい（森田くんは自分のことを独立研究者と言っている。この覚悟も好ましい）。
　鈴木健のことも書いてあった。スマートニュースをおこして成功した起業家だが、当時の彼は森田くんに数学の最初の喜びを教えた大学院生だったのである。カントールの対角線法をプレゼントしたらしい。文系だった森田くんが数学科に転じる気になったのは「健さん」のおかげだったとも書いてあった。
　この「健さん」ともぼくは親しかった。ぼくが加藤秀樹や鈴木寛や上山信一に頼まれてマッキンゼーの会議室でしばらく「半塾」をしていたときの記録係の若き青年だった。のちに週刊アスキー編集長の福岡俊弘の介添で対談をした。あとから、あの対談をしたのは『なめらかな社会とその敵』（勁草書房）を構想中のことだったと聞いた。
　これだけでチューリングと岡潔が並べられるセンスが育まれた背景は説明できないが、そこにアンディ・クラークと荒川修作のブラウザーが関与し、以上の話の途中に出てくるのだが、さらにユクスキュルの「環世界」（Umwelt）の見方が加わってくれば、うんうん、そうだろう、森田くんのセンスの磨き方がよくわかる。

　本書の後半で岡潔に手向けた森田くんの敬意には並々ならぬものがある。日本の数学関係者に岡潔ファンは少なくないけれど、多くの者の感想にはどこか羞じらいのようなものがあった。照れながら褒めていた。理由はわからないでもない。
　岡潔の専門は「多変数解析関数論」である。多変数の解析関数にとりくんだのだが、一変数の解析関数ならコーシー、リーマン、ワイエルシュトラスたちが一望できる理論をつくったけれど、これが多変数になると俄然、難解になる。見える世界の相貌が違うからだ。とくにハルトークスが発見した「擬凸性」（ぎとつせい）が特殊な幾何学性をもたらして、解析関数が見せる存在域がへんてこなのである。
　それでも岡は真っ向から挑み、３度にわたって展望を得た。一度目は擬凸性が解析関数の存在域になっているのかどうかを問うことだった。岡はこれを「ハルトークスの逆問題」と捉えて、存在域の次元を上げて観察するという方法を案出した。関数空間を上から眺めようというのだ。「上空移行の原理」と名付けた。論文は広島文理科大学紀要に受理されたのだが、そのころ親しく一緒に伴走してくれていた親友の中谷治宇二郎（中谷宇吉郎の弟）が病没した。
　二度目は大学を休職して、妻と二人の子を連れて両親の故郷の和歌山県紀見村に移ってからの挑戦だ。３７歳になっていたが、それから畑仕事と数学探求の日々が13年続き、やっと「関数の第二種融合法」をまとめたものの、成果はいまひとつだった。極貧の岡は念仏修行を始め、その日々は農耕と数学と仏道が渾然一体になっていた。
　ここで三度目がやってきた。体の足元のほうから「不定域イデアル」という独得の発想がこみあげてきたのだ。さっそく「層」（sheaf）に組み立てた。岡はこれを「情操による発見」だったと説明した。またのちには、自分のこの発想は「情緒の数学」にもとづいていたとも言った。
　やっと書きあげた「不定域イデアル」の論文は親友の秋月康夫に手渡され、それが渡米する直前の湯川秀樹（６７夜）に託されて、１９５０年のフランス数学会の機関誌に掲載された。世界の数学界が、日本の片田舎にいる数学者に驚いた。ブルバキを代表するアンドレ・ヴェイユ（シモーヌ・ヴェイユの兄貴）がこれを読んで絶賛した。ヴェイユは１９５５年に来日して岡と会い、ヴェイユが「数学はゼロから」と言ったところ、岡は「いや、ゼロまでが大切なんです」と切り返したというエピソードがのこっている。
　というぐあいに、岡の数学は多変数解析関数論の新たな展望をめぐるものであったのだが、本人がそれをもっぱら「情操」や「情緒」で説明したため、日本の数学者たちは褒めにくくなったのである。おまけに岡は数学の本質は「農」に近いとも言ったので、多くのファンは困ってしまったのである。『春宵十話』には、こうまで書いていた。

岡潔の故郷であり数学探求の地ともなった和歌山県伊都郡紀見村（現在の橋本市北部）には、岡にちなんだ「情緒の道」や数学的な偉業を称えるモニュメントなどがある。橋本市役所前にある記念碑には、岡潔の肖像画や肉筆と共に、岡の数学探求の土壌ともなった日本的な情についての言葉も彫られている。

岡潔がパリの留学で得たのは生涯の研究テーマだけでなく、数学探求生活において帆走することになる考古学者の中谷治宇二郎と物理学者の中谷宇吉郎との出会いであった。中谷治宇二郎（図版左上）とは、パリの3年間で学問的な抱負を熱くかわし親交を深めた。37歳から13年におよぶ畑仕事と数学探求の孤高の生活（図版右上）では困窮を極めたが、中谷宇吉郎が褒章を分け与え支えることもあった。文化勲章の受賞後には、岡は中谷宇吉郎を見舞いその報告をした（図版下）。

岡潔は、数学者の高木貞次に宛てた手紙で、多変数解析関数論は数学的自然において四通八達の景勝の地にあると、その数学的な風景について語った。それは、数論、代数学、幾何学、数理物理、数学解析、１変数関数論といった分野と関連するものであった。岡の研究成果は、後世の研究により多領域の基礎となっている。

　ちなみに森田くんの岡潔論は尻切れトンボにおわっていた。岡が道元（９８８夜）や芭蕉（９９１夜）になじんで日本的情緒に浸った根拠を抜き出しそびれたままになっていたのだ。このあたり、武道論や身体論の援用だけでは説明しにくいはずである。たとえば「松のことは松に習え」は、いったん芭蕉の「虚に居て実を行ふべし」のほうに移動しておくべきなのである。
　ついでに言っておくが、森田くんが本書のあと5年をへて上梓した『計算する生命』（新潮社）は、フレーゲを扱っているところが白眉なのだが、その第3章に入るまでが前著の瑞々しさを失っていて、そのためかフレーゲの「概念記法」を称揚するべくその前提に持ち出したカント論の説明に言葉の力が奪われてしまって、その結果、フレーゲの果敢な意図が描出できずにおわっていた。
　できることなら、数学と言語についての議論をいったん展開させ、そのうえで生命論のための数学にとりくんでもらいたい。森田くんならできるはずだ。
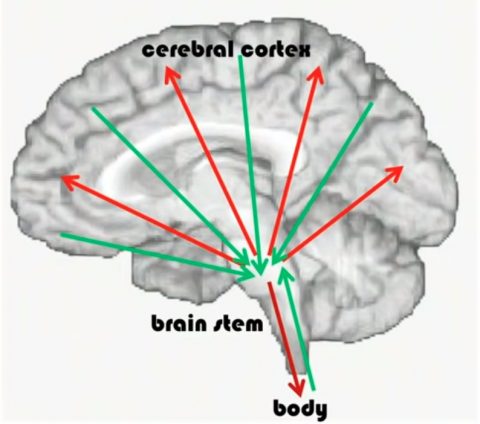
　もう二点ほど、加えておく。ひとつは、本書『数学する身体』は、われわれの行為や思索には数学的なエンボディメント（身体化）がおこっているという重要な示唆によって書かれているのだが、そこにはアフェランス・コピーとエフェランス・コピーがあって、武道家やアスリートやピアニストは、情報操作の指令を脳に頼るのではなく、エフェランスな（遠心的な）膝や手首や指先に托していることが少なくないということである。このことは津田一郎の『心はすべて数学である』（文藝春秋）にも言及されている。私の編集作業も多分にエフェランスにできている。このへんのこと、もっと突ッ込んでほしかった。
　もうひとつは、アントニオ・ダマシオ（１３０５夜）の「ソマティック・マーカー仮説」を“数学的身体観”に加味したらどうかということだ。われわれの思索は身体とともにあるのは当然だけれど、なぜそうなったかということは発生と分化のエピジェネティクスにかかわっているのだし、それが進化のうえで“人体”に及んでいるのだとしたら、脳はその出先を自律分散させたはずなのである。それが「ソマティック・マーカー仮説」だ。千夜千冊を読んでいただきい。

フレーゲは命題が「変項」と「関数」とで構成されていると考えた。「水素ガスは炭酸ガスよりも軽い」という命題を例とすると、「〇〇はXXよりも軽い」が「関数」であり、〇〇やXXが「変項」である。この変項に”水素ガス”や”炭酸ガス”など任意の概念を入れることで、あらゆる命題を作ることができる。
変項という空席を持っているからこそ、関数は多様な意味を表現することができる。この働きは任意の主語を置いて多様な文章を形成できる述語に似ているとフレーゲは考えた。情報の空席をあけておいて、その情報を描写したり移動したりするという考え方は、DNAから遺伝コードを読み取ってタンパク質のもとを運ぶRNAとも近い。

私たちは寝覚めたとき「この私」が「寝る前の私」と同じ人間だと思える。ダマシオはそのような意識の働きが、明確に認識できる部分だけでなく、生命活動のために半ば無意識に動く部分と、そもそも意識になりかけている神経信号の束である部分が重なってできていると考えた。さらにダマシオはこれらを重ねているのは「身体のようななにかのマッピング・イメージ」であると仮説している。数式になる以前の数学的連続性を直感する「数学の情緒」とは、ソマティック・マーカーが察知する”気配”や”目当て”とつながっているのかもしれない。

TOPページデザイン：佐伯亮介
図版構成：寺平賢司・梅澤光由・大泉健太郎
齊藤彬人・中尾行宏

⊕『数学する身体』⊕
∈ 著者：森田真生
∈ 装幀：後藤葉子
∈ 編集：足立真穂

⊕ 目次情報 ⊕
∈ 第一章　数学する身体
∈ 第二章　計算する機械
∈∈ Ｉ　証明の原風景
∈∈ II　記号の発見
∈∈ III 計算する機械
∈ 第三章　風景の始原
∈ 終章　生成する風景
∈∈ あとがき
∈∈ 註と参考文献という

⊕ 著者略歴 ⊕
森田真生（モリタ・マサオ）
1985（昭和60）年東京都生れ。独立研究者。京都に拠点を構えて研究・執筆のかたわら、国内外で「数学の演奏会」「数学ブックトーク」などのライブ活動を行っている。2015（平成27）年、初の著書『数学する身体』で、小林秀雄賞を最年少で受賞。他の著書に『数学の贈り物』、絵本『アリになった数学者』、編著に岡潔著『数学する人生』がある。