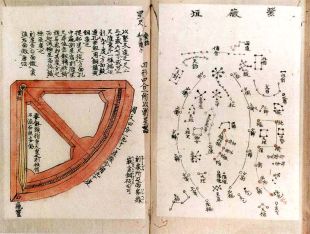
日本の数学 西洋の数学

　そのころのわが家は呉服屋だったから、家中にそろばんが幾つもあった。大きな五つ玉は鬼の子分が履く下駄のようにごっつくて、重かった。ついついスケーターのように片足をのっけて一、二歩滑ってみるのだが何度も転び、そのたびに叱られた。
　父は五つ玉を太い指で操っていた。「二一天作の五、二進が一十」（にいちてんさくのご、にしんがいっし）などと割算九九の二の段をぶつぶつ呟きながら、そろばん片手に伝票を繰ったり帳簿を点検しているのを見ていると、時代劇に出てくる帳場の番頭のようだった。
　五つ玉にくらべると、学校で買わされた四つ玉はスマートで、どこか女の子ぽかった。ラジオではトニー谷というヴォードヴィリアンが片手に持ったそろばんを楽器のように鳴らしながら、「さいざんす、さいざんす」と笑わせて大当たりしていた。

　昭和３０年（1955）がぼくの１１歳である。下京の修徳小学校や中京の初音中学校に通っていた。当時の小中学校ではそろばんはさしずめ今日のケータイやスマホのようなものだったので、全員がランドセルや布カバンにぎゅっと差し込んでいた。
　教室では必ず「そろばんの時間」が用意されていて、見取り算と読み上げ算を一斉にやらされた。読み上げ算は先生がダミ声で「願いましては、いっせんろっぴゃくごじゅうはち円なり、ごまんとんではっぴゃくろくじゅうよ円なり、+++円なり、+++円なり、では」と、次々に数字を羅列しながら読み上げる。教室は一瞬パチパチという音だけになり、できた生徒はすかさずハイ!と声と手を挙げて答えを口上し、先生から「ご明算！」（正解！）と言われてニンマリするのだが、すぐに「ご破算で願いましては」と次の珠算問題が読み上げられる。
　見取り算では配られたペーパーの数字を必死の指捌きでそろばんに入れていく。掛け算、割り算もあり、暗算もさせられた。
　暗算はアタマの中にそろばんを思い浮かべ、そのヴァーチャルそろばんの玉を動かしていく。それができないばあいは、両手を引っ込め、机の上のリアルそろばんをひたすら見ながら「玉を動かしているつもり」になっていく。この「つもり」が厄介だった。
　町の珠算教室に通う生徒も多く、出来のいい子もけっこういたが、これはいまなら電子ゲームが速くてうまい子のようなものだから、めずらしくはない。中学校の同級生には京都の珠算大会で準優勝したヤツがいた。ぼくはそろばんよりも筆算や幾何に向いていそうだったので、中学１年の秋から北大路烏丸の数学塾に週一度だけ通うようになった。出来は悪かった。テストがあったのだが、たしか７０人ほどの通いの中の４６番目だった。

　そろばんは「算盤」と綴る（英語はabacus）。メソポタミアにもインドにも土算盤、線算盤、溝算盤などの独特の算盤があって、「数えて、計算する」という技が文明の初期から芽生えていたことを物語る。中国にはこれらのうちのどれか（おそらくローマの溝算盤）がシルクロード経由で入って、算木（さんぎ）を使う中国式になった。算木を使う算盤はそろばんとは読まずに「さんばん」（スワンパン）と読む。
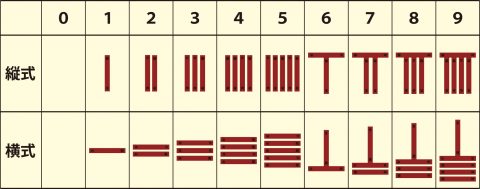
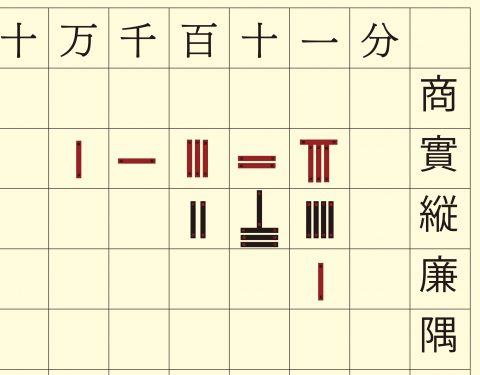
　算木は自然数を最大６本の棒を組み合わせて演算するための計算具のようなもので、小さいものは３～５センチ、大きなものは１４センチほどの木製ないしは竹製の直方の棒をタテヨコに配列した。桁によって算木の向きを変え、赤の算木が正を、黒の算木が負を示した。どちらかというと易の卦（け）のための並べ方に近く、見た目にはやや神秘的で呪能的である。
　儒教や仏教の伝来のあと、そんな中国式の算術書と算木が日本にも届いた。算術書はいくつもあるのでまとめて「算経十書」というのだが、そこには一次方程式（比例算）と二次方程式（ピタゴラスの定理）の解法、面積や体積を求める公式などが述べられていた。祖沖之（そちゅうし）の『綴術』（てつじゅつ）などの高級算術書（円周率について言及）などもやってきた。日本でこれらが読まれていたかどうか、算木がどのくらい使われていたかどうかはよくわかっていない。
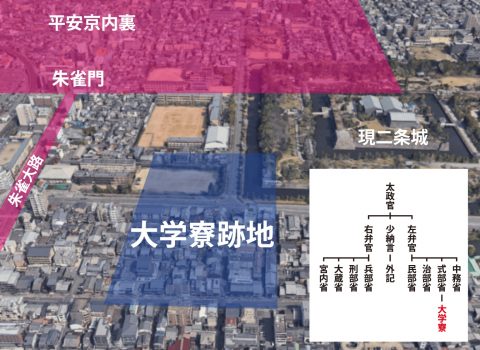
　それでも律令時代になると「算博士」というロールが設けられ、大学寮では明経道・明法道・文章道と並んで「算道」が指南された。後漢時代に編集され『九章算術』をテキストにしたようだ。
　九章というのは、方田（田の面積を求める）、粟米・衰分・均輸（物の売買や税金を計算する）、少広（正方形・四辺形の一辺、すなわち平方根・立法根を求める）、商功（土木工事に伴う体積の計算）、盈不足（分配のための用法および整数論）、方程（連立一次方程式の解き方）、句股（ピタゴラスの定理の説明）など、九つの章で構成されているのでそう称ぶのだが、そのなかで正負のちがい、分数・約分・通分、開平と開立なども案内されていた。
　ただし全体としては問いと答えを示しているだけなので、ギリシア数学やユークリッドのような数学的思索についてはまったく補填されていない。奨励もしない。はっきりいって実用一辺倒なのである。
　なぜ中国の数学がその程度であったのか。それを輸入した江戸時代までの日本の数学も長らく「読み書き、そろばん」と言われていたように、やはり実用一辺倒のままだったのはどうしてなのか。いちはやく数の記号化にとりくみ、世界に先駆けてゼロを発見したインドはどうなのか。これらのことは「アジアの理知と技法」ということを考えるにあたっての、大問題である。
　そもそも東洋や日本は数学や科学に弱いのか、それとも古代ギリシアや西洋とは異なる算術思考や数学思考を育んでいたのか、よくわからない。それについてのうまい説明もない。そこらあたりのことが知りたくて、うずうずしていた時期があった。

算木。赤はプラスを、黒はマイナスを表現している。機械的な操作を算木を組み替えていくことで、桁上がりも正確に計算することができた。計算という概念的操作を、視覚的身体的に捉えることができる手法である。

算木では、図のように0～9を表記する。見まちがいを防ぐため偶数桁の数字は横式で示す。例えば11は「｜－」となる。機械的に計算することを可能にしたわけだ。負の数を初めて使ったのも中国だと考えられている。紀元前207年頃と思われる獣骨製の算木が発見されていて、『老子』にも「善く数うるものは籌索（チュウサク）を用いず」とある。

上図：算木と算盤（さんばん）をつかった器具代数術を籌算（ちゅうさん）という。算博士（サンノハクジ）は算術をマスターするのに、これらを使用した。算盤は布製のものも多く、図版は江戸（1718年）の『正術算学図会』に残された籌算の様子。算博士を輩出した大学寮は、平安京内裏の朱雀門のすぐ近くにあった。当初は選抜試験を受けてその成績に応じた地位に就いたが、平安時代後期には世襲化が進んだ。

日本にやってきたころの算盤で、上の珠が２子、下の珠が５子である。中国では重さの単位として、1斤＝16両であったため、16進法の計算をする必要があった。長崎か堺から入ってきたと考えられているが、この形のままでは定着しなかった。

江戸時代の算盤。日本では16進法は不要だったため、上の珠は１子に減った明式になっている。ただし下の珠は５子のままで、現代と同じ４子になるのは昭和になってからである。

兵学者の松宮俊仍が記した『分度余術』（1728）の表記を図にしたもの。山までの距離が分からない場合でも、△MPQ∽△BECかつ、△NPQ∽△B’E’C’という三角形の相似を使って山の高さが計測できる。実際に1727年に富士山の高さを3886ｍと計測し、実際との誤差は110ｍしかなかった。

『分度余術』の図。実際手に取ることができないようなものを計測するのに、算術は非常に有効な方法であった。太陽の南中高度を測り緯度を求める方法や、北極星の高度を測り緯度を求める方法などが説明されている。

　昭和４０年（１９６５）、文芸誌「新潮」に岡潔（９９２夜）と小林秀雄（９４７夜）の対談が載った。「人間の建設」というおおげさなタイトルだ。ぼくのそろばん時代から１０年後のことだった。
　呉服屋の松岡商店は倒産して、わが家は京都から横浜に引っ越していた。その横浜の借家では回覧雑誌を毎月７～９誌くらい取っていて、そこには両親が読みたがっていた文芸誌もいろいろ入っていたので、ぼくもけっこう目を通していた。それで「人間の建設」も読んだ。日本を代表する数学者と文学者の名人芸が丁々発止しているのだから、おもしろいといえばおもしろかったけれど、カラスミやコノワタをちょいちょい摘まんでいるようで、交わされた中身についてはいまひとつ感動しなかった。
　とくに二人が東洋の知をどう語りたいのかが隔靴掻痒で、なかなか見えない。小林秀雄にあっては半分がたわごとだった。
　それにしても、なぜ東洋の数学的英知というものは析出してこなかったのか、もしくは析出しにくくなったのか。アジア文化には抽象思考が積み上がってこない何かの原因があったのか。やっぱり気になってきた。そこで、あれこれ読むことにした。
　たとえば小倉金之助の『日本の数学』（岩波新書）、サボーの『ギリシア数学の始原』（玉川大学出版部）や『数学のあけぼの』（東京図書）、ボホナーの『科学史における数学』（みすず書房）、薮内清の『中国の数学』（岩波新書）、吉田洋一の『零の発見』（岩波新書）などだ。
　ところが、いくら読んでもいまひとつ要領を得ない。東西それぞれの数学史に寄せるアプローチは詳しく伝わってくるものの、なぜ此彼の相違が出てくるのか、そこが掴めない。このことは20代前半をつかって埋没してみたジョゼフ・ニーダムの大著『中国の科学と文明』全１１巻（思索社）を読んでいても、当のニーダムさんに出会って聞き込んでみたときも（ロウ夫人にもあれこれ聞いてみたが）、わからずじまいのことだった。

小林秀雄と岡潔による対話集『人間の建設』。数学、ゴッホ、酒、ドストエフスキー。東西を横断して主題は目まぐるしく入れ替わり、やがては「無明の明」を巡る。岡潔の目には、功利主義によって没落したローマ帝国と戦後復興を果たしたと浮足立つ日本の姿が重なって見えていた。

上写真は30代半ばのジョセフ・ニーダム。このときにはすでに生化学の大著を書き上げ、その道の権威になっていた。下の写真は『中国の科学と文明』の英語原版と日本語版。日本語版の全11巻（2枚目）がカバーしているのは英語版第4巻まで。1948年のニーダムによる企画立ち上げから70年以上経過した現在、完成を迎えようとしている。

1937年に中国人留学生であったロウ夫人と出会い、中国の科学へ関心を寄せる。やがて、世界をリードしていた中国科学が、その座を西洋諸国に明け渡し衰退した経緯に疑問を抱いた。ニーダムの著述には、洋の東西をまたぐ見方に向かうヒントが詰まっている。写真は、ケンブリッジ大学カイアス・カレッジの入り口を通り過ぎるニーダムとロウ夫人。

　こうしてぼくのこのあとは、東洋思想そのもの、日本文化そのものの秘密を隠しもっているだろう奥座敷に少しずつ踏みこんでいくことになる。老荘、ナーガールジュナ、ヴァスバンドゥ、華厳、タオイズム、また空海、法然、道元、慈円、正徹、心敬、世阿弥、また王陽明、契沖、芭蕉、近松、宣長、梅園、うんぬんかんぬん。
　けれども、これらは東洋的科学知や感性的数学知の解明には直交しにくいものばかりなのである。だったらニーダムのように東洋の科学と技術の特色を今日的に強調していけばいいのかというと、それも容易ではない。
　たとえば古代インド六派哲学にはサーンキヤ学派という算術好きの学派があるのだが（サーンキヤは「数え上げる」という意味）、その中身はプルシャ（精神原理）とプラクリティ（物質原理）によるあいかわらずの因中有果論めく因果論であって、そこから東洋における科学知や数学知の特色をふくらませていくのはムリなのである（９６夜参照、千夜千冊エディション『仏教の源流』参照）。
　では、どこをどう見ていけばいいのだろうか。おそらく東西の思考を同時に見分（見聞）していくという、そういう視座や視点の発動を試みて、そのうえで切り込みどころをつくっていくしかないだろうと思われた。いわば世界比較思想による同時的世界観で東洋や日本を攻めるのだ。中村元さんが挑んできたことだ。
　そんなとき数学関係の本として手がかりになるかなと思えたのが、大矢真一の『和算以前』と村田全の本書『日本の数学 西洋の数学』（両方とも中公新書）だった。どちらも答えが書いてあるわけではないけれど、ぼくの脳裏に僅かな明かりを灯してくれた。
　たとえばプラトンが好んだ立体やユークリッドの『原論』の図形はすべてイデアルな図形なのだが、中国の九草算術が示す図形はたんなる基礎図形にすぎない。いわばコスモロジーから切り離されている。中国にコスモロジーやイデアがないのかと言えば、むろんそんなことはなく、それこそが老荘思想にも華厳宇宙観にも如実なのだが、それにもかかわらず、東洋ではそのことをラショナリズム（合理主義）やアルゴリズム（計算主義）のほうにもっていかなかった。東洋のイデアル図形は大地や身体から取り出さなくとも平気だったのだ。
　古代ギリシア数学はそこが平気ではなかったのである。平気でないからこそ、理念（イデア）が自己運動を始めたのだ。
　今夜は、そのアジア的に平気なところを僅かな明かりで照らして、そこに見え隠れする模様の一端を少しだけ覗いておきたい。その前に、中国の算木数学とそろばん数学のこと、および桃山以降に独自のそろばんを考案して「和算」に向かっていった近世日本の数学事情について、ざっとした特徴を述べておく。

サーンキヤ学派とはカピラ（左図）が開いたと言われるインド六派哲学の一つ。漢訳では数論と書く。サーンキヤとは、数または熟考を意味するサンキヤーsakhyāを意味し、25原理（右図）を数えることで身心と世界を説いた。

　算木による中国数学は「天元術」というものになった。算木を用いた代数で、〈器具代数〉とでもいうべき体系をめざした。天元術は南宋の秦九韶がまとめたもので、元の李冶と朱世傑が『四元玉鑑』や『算学啓蒙』などに発展させた。一次方程式の近似解ならだいたい出せた。
　ところが近世に向うと、この天元術が途絶えてしまう。ひとつには明代で数学を官学からはずしてしまったことが影響し、もうひとつにはそろばんが普及したからだった。代わって程大位の『算法統宗』が一世風靡した。
　天元術が急速に廃れた理由は推測するまでもない。中国数学の真骨頂が〈器具代数〉であったからである。算木という器具が数学思考の中に入り込んで、器具含みの算術的リテラシーになっていたからだ。その算木がそろばんに代わったら、今度はそろばんが器具代数そのものになった。このことは日本の数学が「そろばん数学」「読み書き、そろばん」にすぎなかったこと、基礎リテラシーの技法に徹していたことにつながっていく。

天元術とは、籌算（ちゅうさん）による代数術のこと。問題の答えを「0+x」 の形で仮おきし、これを「天元の一」（てんげんのいち）と呼んだ。本来、1元代数方程式のみを扱ったが、多元連立方程式を扱う二元術・三元術・四元術も生まれた。上の写真のように、暦をつくるための天体観測などにも使用された。また、下図のような三平方の定理なども紀元前2世紀には発見されていた。

天元術によって数学は高度に発達した。左図は朱世傑の『四元玉鑑』（1303年）に掲載された楊輝の三角形。パスカルの三角形と同じ原理が紹介されている。右図は李冶の『測円海鏡』（1248年）の中の、直角三角形内に円を容れる勾股容円問題に属する定理を説明したもの。この本の中で700条に及ぶ定理を述べている。

『益古演段』に収録されている面積に関する31番目の問題。池の直径と土地の長辺と短辺を求めさせる問題。これを天元術と、等積変換の２つを用いて解いている。

『益古演段』の31問目を天元術にして解いている途中の様子。池の直径をｘとしたとき、71歩の2倍からｘを引いたものは、土地の対角線の長さになるので、その平方は（142－ｘ）＾２＝20164-284ｘ+ｘ＾２となる。そこから長辺と短編の差である94歩の平方＝8836を引くと、長方形の面積の２倍が求められる。この、11328-284ｘ+ｘ＾２を現している。

明代になると商業的発展と共に算盤が爆発的に普及した。日本に入ってきたのも丁度このころである。『盘珠算法』（1537年）では、上１子、下５子の明式算盤の使い方が書かれている。明式算盤は、黄龍音の『算法指南』（1604年）が初出。

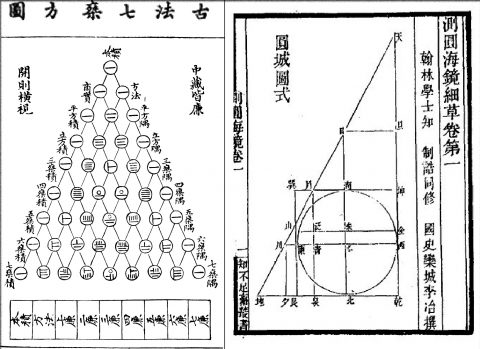
　日本にそろばんが普及するのは、桃山から寛永にかけてのころだ。中国そろばんを改良して玉を菱形立体にした。折からの楽市楽座とともに、そろばんは一挙に普及した。
　毛利重能の『割算書』、百川治兵衛の『諸勘分物』（分とは面積のこと）が一緒に広がり、そこに吉田光由のベストセラー『塵劫記』（1627）が加わって、猫も杓子もそろばん派になっていった。
　吉田光由は豪商角倉（すみのくら）一族で、角倉素庵に『算法統宗』を教えてもらって算数にめざめたらしい。『塵劫記』は一冊の本のことではない。何人もの和算家がさまざまな『塵劫記』を編集した。
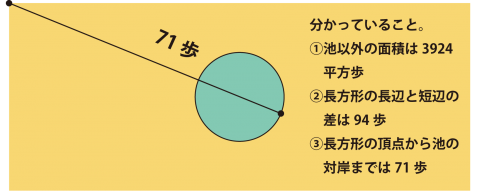
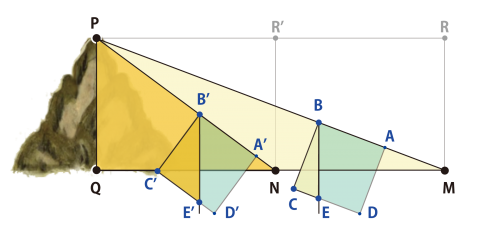
　円周率を求める本も出回った。村松茂清の『算俎』（1663）はπの値を小数第２１位まで計算してみせた（８位以降はまちがっていた）。いつの時代も円や球はマジカルな魅力を持っているものだけれど、徳川期の知識人や民間研究者にとっても円や球にかかわることは人気の営みだったようで、「円理にかかわる者」として一目おかれた。そこでわざわざ解法を人前で見せもした。のちには解法を得意気に絵馬に描いて、寺社に奉納した。けん玉大会に出たり、駅ピで素人を前にピアノを披露するようなものだろう。

『割算書』は、毛利重能による1622年の著書で、著者名が判明している最古の数学書である。九九の割算版である八算、売買、測量などといった当時の算盤に必要な計算が内容にふくまれている。左図は、検地算という項にあるうろこ型の三角形に近い土地の求積の解法。右図は、同じく整っていない土地の面積を区分し求積する計算例。（図版は東北大学附属図書館の写本）

1622年の百川治兵衛の『諸勘分物』は、版元からの依頼を受けて作者が自筆した原稿である稿本として残る最古の数学書である。第一巻は失われており、第二巻のみが伝えられる。佐渡で活動した人物で、佐渡で必要とされた計算の知識がおさめられている。左図は壺、右図は鶴首であり、これらをモデルとした体積の求め方が独特の用語で記されている。（図版は日本学士院所蔵の写本）

『塵劫記』(1627)は、当時のベストセラーともいえる吉田光由の数学書である。独学で学べるように丁寧な説明書きと挿絵が多く盛り込まれる。そろばんによる乗除、比例、利息、求積、測量といった計算方法などの記載があり、何度も改訂版が出版された。1641年には腕利きの挑戦を誘う問題12問を付した版もある。図版は挿絵つきのねずみ算についての記述で、そろばんの教科書的に広まっていた『新編塵劫記』のものである。

　こうした巷の算術熱を背景に、関孝和（1640頃~1708）が登場する。かなりの才能の持ち主だった。筆算による記号代数が独創されたのである。ヨーロッパでも、十六世紀末のヴィエトと次代のデカルトによってなされたことである。
　算木の天元術やそろばんの計算では、一次方程式ならなんとかなるが、これが多元連立となるとお手上げになる。関孝和はそこを工面した。未知数を筆算のための記号係数文字であらわし、そこに補助の未知数を入れられるようにして多元連立方程式を立て、そのうえで未知の補助数を消去して一元方程式で解けるようにした。この解法を「点竄」（てんざん）と言った。
　こうして、文字係数をつかう和算が誕生した。筆と墨でアルゴリズムに挑戦する和算は、見るからに不思議な情緒に富んでいたが、和算そのものは図示の仕方が東洋的なところが特徴なのではなく、その解法が日本的だった。文字係数が仮名やルビの発想に近かったのだ。
　関は処女著作の『発徴算法』でだいたいのアイディアを提案していた。その後の関の和算学は多岐にわたるのだが、その全容は弟子たちによって『大成算経』２０巻にまとまった。

　関の発想は分数式や行列式にも及んだが、西洋数学が導入した「括弧」の使用は思い付けなかった。一方、円理（解析学）にはめっぽう強く、弟子の建部賢弘（１６６４～１７３９）は『綴術算経』に関の円理を発展させた体系を組み立て、もし和算に独自の数学思想があるならこれだろうかという考想を暗示した。「尽」と「不尽」の考想というものだ。
　建部によれば、1/4や1/5は数が尽きる例、1/3や1/7は数が尽きない例で、同様に、加減乗の三つは算法が尽きるもの、除法（割り算）や開平（√Xを開く）は算法が尽きないものだとみなせた。算術というもの、結局はこの「尽」と「不尽」のせめぎあいなのではないかという、そういう考想だ。
　村田全は、はたしてこれが和算思想の到達できた数学思想の姿なのかといえば、ここには西洋数学の「通約不能性」をめぐる深い思索が乏しいと指摘せざるをえないと言うのだが、なるほど西洋数学に照らせばそうかもしれないが、ぼくはここには日本独特の「尽くし」の思想が滲み出ていて、それなりの緩い到達を感じるのである。

関孝和が生前に唯一残した書『発微算法』。天元術では解法がないとされる15の難題全ての解法をまとめたもの。図は最難問の第14問目、1457次方程式を解いている。
右上の図形には甲乙丙などと文字が書かれている。点竄術と呼ばれたこの手法は、数値を文字に置き換えることで算木に頼らず紙上だけで計算＝筆算でできるようにした。この点竄術の発明が起点になって和算の歴史が始まった、とも言われている。

建部は『発微算法』を詳述する『発微算法演段諺解』を著した。関は途中の計算を書かなかった箇所も多く、当時の和算家の不理解を招くこともあった。関の一番弟子であった建部が、関の発見した傍書法（＝多変数方程式）で『発微算法』がいかに解けるのか詳細な解説を与えたことで、関流和算は広く知られるところとなった。

　われわれには「運が尽きる」とか「尽力」という発想がある。これは運や力というものを客観体や客観量の対象として措定しているのではなく、そこにかかわった者たちの営みを関与させて、尽きるものと尽くしえないものを俎上にのせている。
　尽きるといっても、かかわっていくにつれて尽きてきたというニュアンスだ。ここにはモーラ（網羅）の神々にもいくばくかの戯れがあるという見方も出入りする。はたして『方丈記』には「その数ならぬたぐひ、尽してこれを知るべからず」とあった。
　相対化しているのではない。出たり入ったりしているということを観察から外さないのだ。そこは西洋風合理主義のようには冷徹になりきれない。なりきれないのだが、あえて言うなら抽象化をとことん進めるのをためらうのである。ただし、ためらって引き返すのではない。そのうえで飛んで結着させる。そこでケリをつける。
　実は西洋思想や西洋哲学にもこれに似たものがないわけではない。アルキメデスのすだれ論法、カヴァリエリの不可分者の導入、ウォリスの無限算術の方法などだ。詳しくは数式や図解が必要なので、本書61ページ、177ページ、185ページを見てもらいたいのだが、これらは建部賢弘の「尽・不尽」のあいだに少しだけ粗い目のものを入れておくという方法に近いものだった。その粗いものによって、ケリがつけやすくなるのである。
　このようなケリのつけ方はヴィトゲンシュタインについての千夜千冊で（833夜）、ぼくが「カタルトシメス」という風変わりな造語をもって説明した方法にも似ている。ヴィトゲンシュタインは論理によってカタルには（論理で証明するには）、いったんカタル方法とシメス方法とを切断しておいて、そのうえでカタルトシメスという一挙的な新方法で論証と陳述のアンビバレンツに結着をつけるべきだ（ケリをつけるべきだ）と考えた。そんなふうに解説しておいたのである。参考にしていただきたい。

　話を戻して、中国的数学や日本的和算の特徴は算木やそろばんを〈器具代数〉にしたことによって生じたのだろうと思う。アタマと手が器具付き代数としてのみ発展してしまったのである。いったんスマホに慣れてしまうと、誰かと会うのにスマホでメールを送らなければ会えなくなってしまったようなものだ。
　関孝和や建部賢弘はそこを脱して筆算代数に挑んだ。けれども、そこにもまたやはり器具代数化した思索的方法が残響していた。
　東洋、とくに日本においては、アタマの思索は手の手続きなのである。そうなっているため、日本的思索文化は「手続きの作分」のほうを評価する。同時にまた多くの仕事は「道具立てを伴う表現」でなければならなかったのである。
　このことは近代以前の東洋に数学的英知が醸成しなかった理由の説明にはならないかもしれないが、ひょっとすると複雑系の数学や非線形科学の方法や偶有性の哲学においては、意外な相性のよさをもつかもしれないとも思われる。いつか、このことについても解読したい。多少のヒントは津田一郎さんとの対談本『科学、生命、言語の秘密』（文春新書）で話しておいた。ここでは津田さんがデーモンに、ぼくがゴーストに身をやつしながら、科学と文化の、また数学と言語の橋わたしを試みている。

数学を武器に科学的思考を刷新する津田一郎さんと、言葉を道具に編集的世界像をスケッチするセイゴオの間で、ひっそりと愉しんできた対話が公開された。理科系・文科系が融合した世界観の先にゆらりと現れる、科学と生命と言語の秘密を巡る。鍵になるのは、科学の中で仮想されてきたデーモン、物語のうちに写しとられてきたゴーストの痕跡を嗅ぎとろうとする構えそのものだ。みんなにももっと、化けて出てほしい。
撮影：後藤由加里

1864から1865年の間に渋谷区・金王八幡宮へ奉納された絵馬。大中小の三円が互いに外接する図を中央に示し、小中の二円の半径が与えられたときの大円の半径を問うている。左側には三平方の定理を応用して得られた解が端的に記される。1864から1865年の間に渋谷区・金王八幡宮へ奉納された絵馬。

1865年に岐阜県大垣市の明星輪寺に奉納された絵馬。右から三番目の図形問題は「河合澤女」という名の16歳の少女による出題だが、難易度は現在の大学数学専攻以上。和算は年齢性別の垣根を越えた遊芸の対象だった。

岐阜県養老町の田代神社の算額。天保12年（1841）に奉納された。全部で５問あり全て図形問題。右から2番目の問題は、黒い部分の面積が分かったとしたら、朱色の円の直径はどれだけなのかを聞かれている。次の図はその解答。これらの問題はすべて、12歳ほどの童たちによって解かれている。

現代でも算額の文化は続いている。図は、東大寺で平成28年に出題されていた算額。東大寺に残る『華厳五十五所絵巻』にちなんでいる。55か所の頂点を持つ多面体の最小面積を求める問題。

TOPページデザイン：富山庄太郎
図版構成：寺平賢司・梅澤光由・大泉健太郎
齊藤彬人・中尾行宏・上杉公志

⊕『日本の数学 西洋の数学　―　比較数学史の試み』⊕
∈ 著者：村田全
∈ 編集：加納信雄
∈ 発行者：嶋中鵬二
∈ 発行所：中央公論社
∈ 本文印刷：三晃印刷
∈ カバー印刷：大熊整美堂
∈ 製本：小泉製本
∈ 発行：1981年

⊕ 目次情報 ⊕
∈∈ はしがき
∈∈ 目次
∈ I章　課題と展望
∈∈ 1　数学の何をどう比べるか
∈∈ 2　円周率をめぐる歴史の概要
∈∈ 3　曲線の長さ、曲線図形の面積
∈∈ 4　理論的世界とその背景
∈ II章　西洋数学の源流
∈∈ 1　『原論』以前のギリシア数学
∈∈ 2　ユークリッドの『原論』
∈∈ 3　『原論』と通約不能量の理論
∈∈ 4　『原論』の論証法――エレア学派の論理思想
∈∈ 5　ピュタゴラス、プラトン、アリストテレス
∈∈ 6　アルキメデスの数学
∈∈ 7　アルキメデス以後のギリシア数学
∈∈ 8　インド、アラビアの数学的伝統
∈ III章　和算の形成とその性格
∈∈ 1　平安時代までの日本の数学
∈∈ 2　和算の源流――シナ数学の伝統
∈∈ 3　和算誕生への道
∈∈ 4　初期の和算――円周率をめぐって
∈∈ 5　関孝和の業績
∈∈ 6　建部賢弘の方法
∈∈ 7　松永良弼と久留島義太
∈∈ 8　和算のその後
∈ IV章　近世ヨーロッパの数学
∈∈ 1　西洋中世の意義――西洋近世数学の思想的背景
∈∈ 2　記号代数学への道
∈∈ 3　求積問題の新展開
∈∈ 4　ウォリスの『無限算術』
∈∈ 5　接線問題の諸相
∈∈ 6　微分積分学の基本定理
∈ V章　比較数学史について
∈∈ 参考文献
∈∈ 略年表

⊕ 著者略歴 ⊕
村田全（むらた・たもつ）
1924年（大正13年）、兵庫県に生まれる。1948年北海道大学理学部卒業。同大学教授を経て桃山学院大学文学部教授。1994年定年退職。立教大学名誉教授。専攻、数学思想史。著書に『数学史散策』（ダイヤモンド社）、『数学史の世界』（玉川大学出版部）、共著に『数学史』（筑摩書房）、訳書にブルバキ『数学史』（共訳、東京図書）、ボホナー『科学史における数学』（みすず書房）、カントル『超限集合論』（共役、共立出版）ほか。