書き手はベルギー生まれの数理物理学者。少しばかりユーモアがある。統計力学をブリュッセル自由大学で修めてプリゴジン（９０９夜）らと多少の丁々発止を愉しみ、60年代にプリンストン高等研究所に招かれ、その後はフランス高等科学研究所で理論物理学を指導した。ヨーロッパにおけるカオス研究の草分けだ。
本書は柔らかな説得感が揺蕩(たゆた)った一冊で、３０年ほど前に初版で読んだときの体感のようなものがいまも残る。もっとも本人はアタマに浮かんだ説明手順のまま綴っているようで、話のアトサキをこだわっていない。すこぶる連想的なのだ。おそらく推敲しないまま仕上げたのではないかと思う。
この本のあとに書いた『数学者のアタマの中』(岩波書店)でも、その柔軟なほろ酔いかげんめいた書きっぷりが躍如して、あいかわらずいい気分にさせてくれた。
中身は、偶然を相手にした科学は何を考えようとしてきたのかということをめぐっている。タイトル通り、「偶然についての科学」がどのようにカオス理論や非線形な数学になっていったのかという、お話だ。
ヨーロッパにおいて、最初に偶然と手合わせしようとしたのはパスカル（７６２夜）、フェルマー（４３５夜）、ホイヘンス、ベルヌーイたちだった。かれらは、コインのトスやサイコロの振りのように何度もくりかえされる事象や現象が、当初はおよそ不確かな予想しかつかないのに、くりかえしているうちになんだか「大きな系」にかかわっているような気がしてきて、そのうち無秩序の中に秩序のようなものが見えてくるのはなぜかということを考えた。
この先駆者たちの偶然性の研究が下敷きになって、やがてそこからラプラス（１００９夜）の確率論やボルツマンの統計力学が生まれてきた。これらの学問は「偶然を飼いならした学問」なのである。本書はその飼いならし方の変遷を、ひらりひらりと話題を移しながら解読する。
ちなみに哲学や社会科学では偶然がどう扱われていたかというと、本書では何も言及していないが、そうとう手ひどいものだった。たとえばスピノザ（８４２夜）のばあいは「あるものが偶然と呼ばれるのは、われわれの認識に欠陥があるからにすぎない」だし、ヘーゲル（１７０８夜）は「哲学的考察は偶然的なものを排除する」である。幾何学に関心があったフッサール（１７１２夜）でさえ「現象学の領域にはいかなる偶然も存しない」だった。
ヨーロッパ哲学は偶然を苦手としたのである。例外はライプニッツ（９９４夜）、シェリング、ショーペンハウアー（１１６４夜）、ニーチェ（１０２３夜）、ジンメル、ハイデガー（９１６夜）、メルロ＝ポンティ（１２３夜）あたりだが、しかしそのいずれもが九鬼周造の偶然をめぐる考察には及ばなかった。千夜千冊で木田元の『偶然性と運命』（１３３５夜）と、九鬼周造の独特の偶然哲学（６８９夜）をまとめておいたので、よかったら参照されたい。
著者のルエールは、ベルギー出身のフランス人で数理物理学者。力学系における創発的ふるまいを純粋数学であらわし理論にしてきた。フローリス・タケンスと共にストレンジ・アトラクターという言葉を生み出し、乱流の新しい理論を開発した。
1654年、パスカルとフェルマーは、貴族のシュバリエ・ド・メレというギャンブラーがサイコロ賭博で身を滅ぼしたことを論じ合い、ベルヌーイも関心を寄せた。確率論は、「十分に長い間ゲームを続けたときに確実に勝つためには、賭け金をどのように調整したらよいか」といった実際問題からおこった。図版（『数学の世界』）は、３つのサイコロを振った場合の出目のパターンとその確率である。サイコロを一度振るだけの結果は不確かだが、何度も繰り返して観測することで偶然性がある確率に収束していくようすが見える。
さて、偶然をめぐる科学は何を考えたのかというと、一言でいえば、偶然に見える現象や事象には、もともと「でたらめ」(無秩序性)や「たまたま」(偶発性)というものが入っていたとみなしたのである。
ボルツマンが熱力学の第二法則や統計力学を確立しようとしていた時代、科学者は「１リットルの空気の中では、たくさんの分子があらゆる方向に猛烈なスピードで飛び回り、そこでは驚くべき無秩序さで互いがぶつかりあっている」というフィジカルイメージを抱いていた。まだ素粒子や量子の科学が登場していない１９世紀半ばのことだ。
ここで「無秩序さ」と言っているのは今日の言葉でいえばカオス分子というもので、１リットルの体積の中にたくさんの「でたらめ」があるということだ。そこには「でたらめ」を惹起させていく「たまたま」がひそんでいるというイメージだ。
ボルツマンやギブズは、この「でたらめ」の淵源の動向をエントロピーと名付けて偶然性の担い手と見立て、そもそも宇宙や自然はこのエントロピーという無秩序さ具合によって出来上がっているのだろう、ただし何かの事情でこのエントロピーの値は変化するのだろうと考えることにした。こうして詳しいことはあとまわしにして、エントロピーは「でたらめさ」や「無秩序さ」の加減のことだと定義された。
何かの事情のほうは、このあと熱力学の事情によっていることが明らかになった。ボルツマンは科学史上最も重要な熱力学第二法則を発見したのだが、このこの法則は「すべての物理現象においてエントロピーは一定であるか、または増大する。増大する過程は非可逆的である」ということを主張していた。多くの科学者たちがギョッとした。偶然性とエントロピーは熱力学的な変化にディペンドして、無秩序さと秩序っぽさを見せていたのである。
ここで科学者と数学者は、あることに気がつく。エントロピーが上がったり下がったりしながら切れ目なく変容しているのだとすると、そのもともとの初期状態はどういうものなのか、もしその系の初期条件が少し変われば、その後の秩序っぽさにも変化があらわれるんじゃないか。となると、世の中には初期条件に強い依存性をもつ系があるんじゃないか。そういうことに気がついた。
２０世紀になって、このことは生命系にこそあてはまると考えられるようになった。シュレディンガー（１０４３夜）は「生命は負のエントロピーを食べている」とみなし、プリゴジンは地球が熱力学的な非平衡系であることを証した。
ボルツマンの墓にはエントロピーＳを求める公式が刻まれている。マクロな物体間に生じる乱雑さとして用いてきたエントロピーを、ミクロ世界の原子・分子レベルでの乱雑さにもあてがった。熱力学から統計物理学へ地をうつしたのだ。
話を戻して１９世紀末、フランスの数学者ジャック・アダマールは負の曲率をもつ面の上で点が摩擦なく動くとしたらどのように運動するのかを調べた。測地流という動きである。調べてみると、点は初期条件に強く依存することがわかった。
これを承けた物理学者のピエール・デュエームは、アダマールの測地流の軌道を予測する計算をいくら組み立てようとしても、初期条件に含まれてしまうらしい小さな曖昧さのために、軌道の予想ができなくなることを確認した。
同じころの１９０８年、アンリ・ポアンカレ（１８夜）は『科学と方法』のなかで、予測不可能性とは何かという問題をプリンを掬うようにとりあげて、こう書いた。「われわれの目をかすめるような小さな原因が、無視できないほど大きな効果を生むことがある。このとき、その効果は偶然に起こったと言われる」。
ポアンカレは古典的決定論と確率論的な理想化による推論とはべつに、初期条件に強く依存する運動がありうることを予告し、その例として「衝突」と「気象」を挙げた。その後のカオス理論に至る科学の前線は、このポアンカレの指摘に沿うように進み、まずは「乱流」があらわすモードを着目するようになった。
乱流は見つけるのはたやすいけれど、その性質を理解するのは難しい現象である。ポアンカレは流体力学にとりくんで渦についての講座を担当し、ハイゼンベルク（２２０夜）も乱流理論の構築を試みたことがあったのだが、広く受け入れられることはなかった。「乱流は理論家の墓場だ」とさえ言われた。
しかし、乱流は何かを興奮させる。レオナルド・ダ・ヴィンチ（２５夜）の乱流スケッチはその興奮を如実に伝える。レイノルズ、テイラー、カルマン、ルレイ、コルモゴロフ、クライクナンらの流体力学研究は、その興奮の原因になんとか肉薄しようとするものだった。
本書の著者のルエールも、五月革命の最中にランダウとリフシッツの『流体力学』を読んで興奮し(翻訳は東京図書で2冊本になっている)、乱流の始まりに目を向けるようになったらしい。ブリュッセル自由大学の数理物理学の父と言われていたテオフィル・ド・ドンダーに感化されて読んだ（アインシュタイン（５７０夜）はド・ドンダーのことを「小さな重力博士」と呼んでいた。小柄だったからだ）。
では、ランダウが示していた乱流の始まりには何があったのか。「モード」の劇的な変化があったのである。
レスター写本に残された、レオナル・ド・ダヴィンチによる2枚のスケッチ。濠の中に落下する水の渦と、流水が柱の裏側で乖離乱流になる様子を描いている。レオナルドが注目したのは、無限のパターンを持つ、カオティックな螺旋だった。
物理学においては、モードとは周期運動のことである。振り子、金属の棒、楽器に張られた弦は、叩けばすぐに周期的な運動を始める。これがモードだ。オルガンのパイプの中、吊り橋、ハーモニカ、自動車のノッキングにも、振動モードがある。固体の中の原子が平均の位置のまわりで振動するときのモードは「フォノン」という。
ランダウは、流体が外力を受けて運動を始めるとモードが励起される様子を研究した。モードが一つも励起されなければ流体は安定している。モードが一つだけ励起されれば流体は不規則な運動を始める。たくさんのモードが励起されたとき乱流になる。ランダウはこのことを数学的にあきらかにした。ランダウとはべつに、ドイツの数学者エーベルハルト・ホップも似たような理論を発表した。ランダウとホップの理論は「乱流の発生」を説明しているようだ。
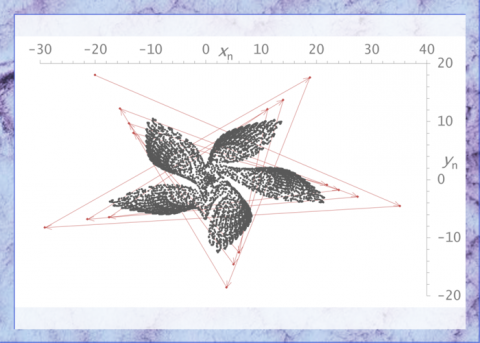
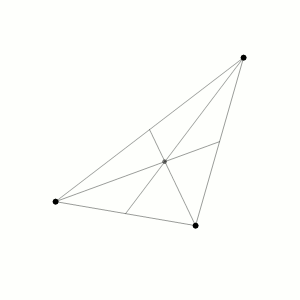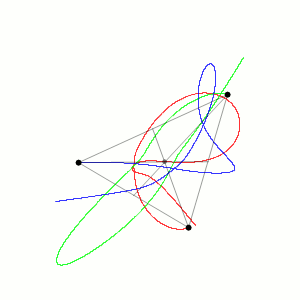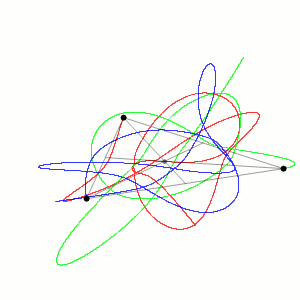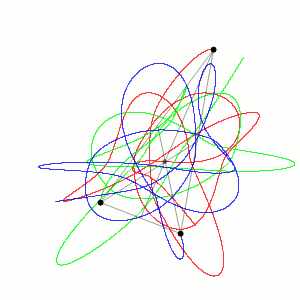
ところがルエールは、この理論の説明に納得がいかないものがあるように感じた。そしてそのことをオランダの数学者フロリス・ターケンスとともに「乱流の性質について」という論文にして、そこにはストレンジ・アトラクターによる乱流の説明の可能性があるのではないかと提案したのである。
数学は数式や定理の寄せ集めばかりでは組み立てられない。幾何学化をするべきときがある。現象や運動を空間の点の動きとして数学的に視覚化するという方法だ。
ルエールはこの方法を乱流の説明でこそいかすべきことをポアンカレに戻って学びなおし、乱流がモードの重ね合わせでは説明できない奇妙な(ストレンジな)運動性にかかわってアトラクターを形成していることを図示した。
アトラクターとは、いま扱っている系をあらわす点Pが長い時間を経過したのちに、過渡現象が消え去ったあとでも通る点の集合のことである。そういうモードのことだ。これがアトラクターの定義だが、条件がある。系に作用する力が時間に依存しないこと、その系は散逸系であるということだ。
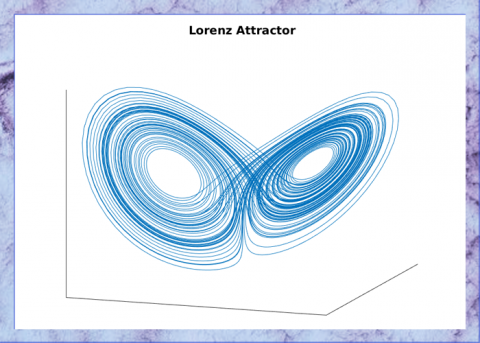
ルエールは、このようなストレンジ・アトラクターがすでに気象学者エドワード・ローレンツによって提示されていたことに大きな興味を抱き、ローレンツがコンピュータによって示した美しくも不思議な模様をもつローレンツ・アトラクターが、メリーランド大学の応用数学者ジェイムズ・ヨークによって「カオスが創発しているパラダイム」の最も典型的な例だと指摘されたことに、さらに興味を募らせた。
乱流の正体をめぐる探索から、なんとカオスが躍り出てきたのだった。しかもそのカオスは初期条件に強く依存するような時間発展系に属していた。偶然は必ずしも飼いならされていたわけではなかったのである。偶然はカオスが律していたのかもしれなかった。
世間がざわついた。経済の活動や脳の活動にもカオスが関わっているのでないかという期待が膨らんできたのだ。世の中というもの、不確実なことだらけであって、カオスを研究すれば不確実な動向になんらかのメドが立つのなら、ここにもそこにもカオスを見出したくなるのも人情だ。
茶目っ気もあるルエールは小躍りするように、本書をカオス三昧な話でおもしろがらせようとする。おもしろがらせようとするのだが、釘も刺す。生物学や生態学や経済学がカオスの研究をする場面での準備不足についての注文だ。
ローレンツ・アトラクターは、数学者・気象学者であるエドワード・ローレンツが1963年に発表した。もともとは大気対流を数学モデル化し、３つの「非線形常微分方程式」として記述した決定論的な系であるが、ローレンツはこの系が初期条件に対して鋭敏な依存性を示すことを実証し、カオス研究に端緒をもたらした。
ストレンジ・アトラクターとは、カオス理論の研究の中で発見された奇妙な挙動を示す微分方程式の状態の総称。図版は、適当な初期条件を与え、写像を繰り返し適用することで多種多様な形状を現すグモウスキー・ミラの写像の一つ。ミラはこのアトラクターを「神話の鳥」と命名した。
うまく選べば、ストレンジ・アトラクターは複数個合成することができる。画像は2〜3つのアトラクターをプログラムによって合成し、出力した例。あたかもラスキンの絵画のような、淡い塵じみた図形が出来上がる。
上田 睆亮（うえだ よしすけ）は、1961年に世界で初めて物理現象としてのカオス現象を発見した。右はその時の電気回路の周波数引き込み現象を記述する非線型常微分方程式のシミュレーションにおいて得られたグラフ。上田は、ありふれた自然現象であるにもかかわらず、その概念把握の困難さのために、カオスは見過ごされてきたと語っている。
ダフィング方程式で現出するストレンジ・アトラクターの一つ。命名したのはフランスのダヴィッド・リュエル。発見した上田睆亮に因んで、ウエダ・アトラクタとも呼ばれる。リュエルは1978年に、エドワード・ローレンツに先立って上田がカオスを発見したことを報じた人物である。
カオス研究では、その系のダイナミクス(動力学)が定量的にわかっていなければならず、そのためには系の現象の時間発展を記述する基本方程式がよくわかっていなければならない。数学的には、その方程式がコンピュータによって精度よく積分できなくてはならない。
それがあらかじめできるのは、わかりやすいところでは太陽系天文学や流体力学や気象学である。そのほかの、たとえば振動する化学反応や生命体の現象などでは、そもそもの基本となる運動方程式がわかっていないことが多く、長い時間におよぶ時系列の動向を確保することも難しい。とくに生物学が対象とする「柔らかい科学」では、時間発展の基礎方程式が時間とともにゆっくり変わってしまうことが少なくない。系が学習して適応力を発揮するからだ。そこに仮に初期条件に敏感に反応するカオスがはたらいていたとしても、そこからダイナミックな定量変化は容易には得られない。
経済学が景気や物価の動向を予測しようとするばあいも同様で、初期に設定された金利が経済の全体動向のどこを動かすかは、なかなか予想しがたい。そこでサンタフェ研究所のブライアン・アーサーなどは『テクノロジーとイノベーション――進化／生成の理論』(みすず書房)を書いて、経済政策のためのカオス研究ではなく、むしろ日進月歩で変化するテクノロジーのデータを十分に検討することによって、経済が出くわすカオスを想定する試みを組み立てたのだが、ルエールはその試みの方向を応援しつつも、やはりカオスの創発を経済界や技術界が観察できるようにするには、そうとうの難関が待っているだろうと、しぶちんな判定をしてみせたのである。
こうして本書は後半戦を、量子力学とカオス、エントロピーとカオス、情報とカオス、複雑系とカオス・・・という順で読者を導いていく。ルエールがこんなふうに話題を並べたのは、偶然というものはいろいろ姿や形を変えてあらわれるものであるが、とはいえその正体にアプローチするには手立ての数学が必要で、それにはまず量子力学が先行したのでそのことを理解したうえで、その数学的な考え方をつかいながら、いったいわれわれはポアンカレの先導でカオスを発見できたことによって、いったい何に肉薄しようとしているのか、それは情報の本来の正体ではないかということを、言いたかったからである。少しだけかいつまんでおく。
量子力学で基本になるのは「確率振幅」である。量子のふるまいを確率統計的な振幅として捕捉しようとするものだ。この振幅は複素数であらわされる。量子力学の数学でわかることは、この振幅がどのように時間発展するかということだ。そのことを示しているのがシュレディンガー方程式(確率振幅を解くための波動関数)である。量子の動向はこれによって量子の状態の数としてわかることになる。
量子力学の数学にはオブザーバブルという量が出てくる。線形演算子のことで、量子力学では一つのオブザーバブルと一組の振幅が与えられれば、その後の振幅のことは決定論的にわかる。決定論的にわかるのだが、確率振幅としてしかわからない。エネルギーが量子化されているので、粒子のエネルギーはとびとびの値でしか明示できないからだ。
決定論であって、確率論的であるとはどういうことなのか。ひとつには、量子力学が扱う物質の動向は月水金が粒子っぽくて、火木土が波動っぽいということだ。ここには「AかBか」と「AかつB」が共存している。もうひとつには、量子力学の数学では粒子っぽいところから波動っぽいところに移るところは(その逆も)、量子力学ではまったく取り扱われていないということである。AがAであり、BがBであることは不問にされていて、おまけにAがBの状態になるということを説明しようとはしていないということである。
話はここで転換する。われわれは熱が冷えると水が氷になり、熱が上がるとお湯になるという物理現象を、いまだ一度も物理学で説明できてはいないという話になる。この現象は「相転移」という名がついているものだが、このことを証明する物理学はない。低温で結晶化することを数学的に証明できる原子や分子の状態を、ただの一度も明確にしたことはないのだ。
ところが、ところがである。われわれはカオスの出現を数学的にあらわすことができたのである。ストレンジ・アトラクターが推移してカオスとしての顔を見せたときには、その系になんらかの情報が創発していることを確認できるようになったのだ。
これはAかBかとAかつBを説明することにもならないし、相転移をカオスの創発で説明することにもならないのだが、そういうことを超えた構想が示唆されているとも思える。どうもこれまでの科学的な説明の仕方をがらっと変えたくなるような、いわば偶然と必然のあいだにまたがる情報のふるまいの謎に関する根底的な考え方に出会ったことを示唆しているようにも思えるのだ。
たいそう無責任な話だがも、諸君、そう思いませんか、ルエールはそう暗示して、本書の結末をなんだかルンルンした風情で閉じてしまうのだった。
こんなことを最後の最後になって書いている。・・・物理的宇宙にはでたらめなところがたくさんあるし、数学の主張には証明できないものがたくさんあるけれど、それでも物理的宇宙や数学について、これほど多くのことが理解できるのは、この理解のありかたが人間の知性が本来もっている特殊な性質と強く結びついているからなのだ。・・・たとえば数学は自然言語もつかっているが、これは数学そのものがめざした形式言語ではなく、いわば略式(セミフォーマル)を装うことにしたからだ。そのぶん、人間は数学的知識を簡潔な定理にしていくことを選んだのだ。・・・そうだとするなら、数学的世界には、われわれという実在と数学的な実在者がいるということになる。「群論と量子力学」のノーベル賞科学者ユージン・ウィグナーはそのことを、かの「自然科学における数学の理不尽なまでの有効さ」にとっくに告白していたではないか。
マンデルブロ集合はビジュアル化されたカオスである。ある関数の初期値を変えた場合、初期位置から点が移動した先が同じ一箇所にとどまるか、無限大の彼方に飛ぶかが色分けしてマッピングされている。マンデルブロ集合は自己相似という性質を持ち、右に倒れたハートと円をくっつけたような漆黒のシルエットは拡大するといたるところに発見できる。
図は三体問題の近似解の一例。三つの質点が複雑で不規則な運動をすることが分かる。アンリ・ポアンカレは三つの天体の運動を解析的に解くことはできず、そこには予測もつかなかった運動が見られることを証明した。図のように軌道をシミュレーションするには、何らかの仮定（制限）を加えなければならない。
流れのなかに障害物があるとき、物の後方に交互に渦構造が発生することをカルマン渦という。図は野球で魔球とされるナックルボールの挙動をシミュレートしたもの。回転しないボールと流体間の摩擦により背後に生じたカルマン渦がボール自身を揺さぶり、そのことでさらに大きな渦が生じる。
格子振動とは、結晶中の原子が、それぞれの安定な位置（格子点）の周辺で行う微小な振動である。フォノンとは、その格子振動を量子に準えて量子化したエネルギー量子（とびとび、基本量の整数倍）である。格子がエネルギーを吸収すると励起されて、図版のように別の振動モードに切り替わっていく。フォノンには、固体を伝わる音波の粒子という意味がある。
TOPページデザイン：松田行正
図版構成：寺平賢司・梅澤光由・大泉健太郎
中尾行宏・桑田惇平・齊藤彬人
⊕『偶然とカオス』⊕
∈ 著者：ダヴィッド・ルエール
∈ 訳者：青木薫
∈ 編集：吉田宇一
∈ 発行者：安江良介
∈ 発行所：株式会社岩波書店
∈ 印刷：三陽社
∈ カバー：半七印刷
∈ 製本：松岳株式会社
∈ 発行：1993年
⊕ 目次情報 ⊕
∈∈ はじめに
∈∈ 謝辞
∈ １ 偶然
∈ ２ 数学と物理学
∈ ３ 確率
∈ ４ 宝くじと星占い
∈ ５ 古典的決定論
∈ ６ ゲーム
∈ ７ 初期条件への依存性
∈ ８ アダマール、デューエム、ポアンカレ
∈ ９ 乱流―モード
∈ 10 乱流―ストレンジ・アトラクタ
∈ 11 カオス―新たなパラダイム
∈ 12 カオス―その後
∈ 13 経済学
∈ 14 歴史の発展
∈ 15 量子―基本となる考え方
∈ 16 量子―状態の数をかぞえる
∈ 17 エントロピー
∈ 18 非可逆性
∈ 19 非衡系の統計力学
∈ 20 沸き立つ湯と地獄の門
∈ 21 情報
∈ 22 アルゴリズムの複雑さ
∈ 23 複雑さとゲーデルの定理
∈ 24 性の本当の意味
∈ 25 知能
∈ 26 エピローグ―科学
∈∈ 訳者あとがき
∈∈ 注
⊕ 著者略歴 ⊕
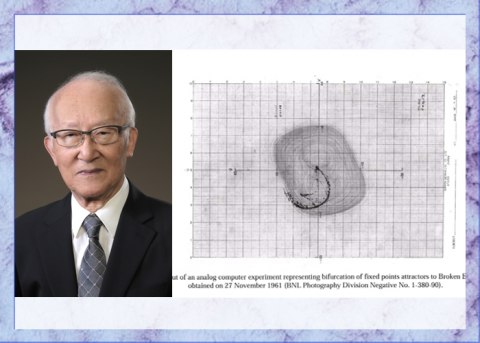
ダヴィッド・ルエール（David Ruelle）
1935年、ベルギー生まれ。カオス研究の草分けとして有名なフランスの数理物理学者。1957年、ブリュッセル自由大学卒業。1959年、物理学でPh.D.を取得。1962-64年にはプリンストン高等学術研究所に招かれる。現在はフランス高等科学研究所の理論物理学の教授。1985年にハイネマン賞、1986年にボルツマン・メダル賞を受賞。著書に『数学者のアタマの中』（岩波書店、2009）他。
⊕ 訳者略歴 ⊕
青木薫（あおき・かおる）
1956年生まれ。翻訳家。訳書に『フェルマーの最終定理』『暗号解読』『宇宙創成』などサイモン・シンの全著作、マンジット・クマール『量子革命』（以上、すべて新潮社）、ブライアン・グリーン『時間の終わりまで 物質、生命、心と進化する宇宙』（講談社、2021）、トマス・S・クーン『新版 科学革命の構造』（みすず書房、2023）他。
