カオスとフラクタル

　いまとなっては尊い一冊だ。非線形な板場の数学俎板に生きものじみたカオスを次々にのせて、これを味にうるさい客の前でみるみるおいしく料理しようというのだから、誰もができる芸当ではない。書き下ろしだろうが、愉快な語り口で屈託なく書いている。これが山口昌哉の数学的悦楽なのかと思わせた。
　父君は日本画家の山口華楊である。竹内栖鳳や西村五雲ゆずりの花鳥画の名人だった。おじいさんは京友禅の職人で、山口家は中京にあったから、ぼくの父はその仕事ぶりを知っていた。
　そんな家に育った山口が昭和２２年に京大理学部の数学科を卒業し、曲線には長さがあるけれど、ある領域の境界には長さがない曲線があってもいいじゃないかと思い始めてから、変になった。大学院を出てから工学部に移り、非線形振動をいじるようになって「引き込み」を計算するうちに本気になり、南雲仁一から頼まれて神経数理モデルの手伝いをしていて、もっと変になった。抗原抗体反応の数学にとりくんでいたらしい。フランスにも留学した。
　それからは理学部に戻って、岡田節人や寺本英の研究室と生物数学のコラボレーションをしていたようなのだが、そのとき若い研究生たちからリー（李天岩）とジェイムズ・ヨークのカオスの論文を見せられてガーンときた。たちまち「これや！」と思ったという。「こんなおもろいもんはない。なんで気がつかへんかったのやろ」というほどの、どんぴしゃ感だった。それが５０歳のときなのである。以来、山口先生といえばカオスの数学となった。
　本書は、その「これや！」の感触を、評判の板長がまじまじと蘇らせるように披露した尊い一冊だ。講談社のブルーバックスで刊行されたのち、ちくま学芸文庫に入った。校勘を頼まれた合原一幸が解説も書いていて、これがまたなんとも慈愛がこもっていて、うるうるさせた。山口先生は書きっぷりがやんちゃなせいで、いろいろなまちがいを゙平気で語りつづけるところもあるのだが、これは先生の「おおらかさ」でもあるのだから、できるだけそっとしておいたというのだ。たしかにそうなっている。

山口昌哉は旧制第三高校から京都大学理学部数学科に入学。工学部に転属した助手時代に、上司から強制振動問題を持ち込まれ非線形に取り組む。やがて、人生や生命を思わせる非線形のふるまいに魅かれていく。「無責任、無節操、破廉恥」が学問研究のモットーだと豪語していた。

メリーランド大学のヨーク教授と大学院生リーは、1975年に「リー・ヨークの定理」を収めた『Period three implies chaos』を発表した。数学の言葉として史上初めて「カオス」が用いられた論文である。二人の成果はローレンツとロバート・メイの研究に励まされたものだった。

　水道の蛇口をあけて１分間に０・４リットルの水を水槽に流していくと、水槽の水の量は時間経過ｔと比例関係になる。直線グラフで描ける。１時間後の水槽の水の量をぴったり予測することもできる。ここには線形的な法則が成立している。
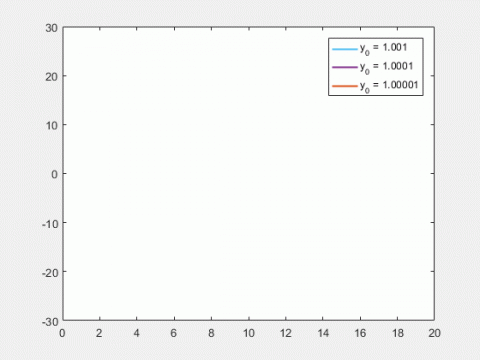
　すでに水槽に９リットルの水が入っているとすると、この９リットルの水は最初に与えられた量なので、初期値とか初期条件という。初期値を決めておけばｔにおける水量は必ず決定する。こういう決まり方をする法則は決定論的な法則である。これに対してサイコロを投げて目がどのように出るかというプロセスは、たくさんのデータをとっても決定論的な法則にはならない。初期値が何であれ、確定的な将来像は描けない。描くとすると確率的な表現になる。これは非決定論的なプロセスを著している例なのである。
　パイの生地を練るには、バターを含んだ材料の粉のかたまりを捏ねたり拡げたり、二つに分けたり巻いたり折り返したりを繰り返す。すべての生地が均一になってくれば、出来上がる。とはいえ、その中の１点がどう動いたかをすべて記述するのはたいへん複雑で、容易ではない。この例は「パイこね変換の力学系」としてよく知られたものなのだが、初期条件の少しずつのズレが指数的に増大していくので、初期値がもたらす影響を議論するのによく引き合いに出されてきた。パイ生地の中の１点がこの系のあらゆる点に対応して動いたかのような印象があるため、エルゴード性が成立している例としても、原子間の反応の非線形性を説明するばあいの例としても、よく持ち出される。
　本書はいま述べたような例を最初にいくつか持ち出して、わかりやすい数式を擬きながらするすると説明てみせ、しだいに決定論と非決定論のちがい、線形性と非線形性のちがいを際立たせていく。やがて、このような考え方や数学的な使い方から、どのようにカオスが話題になってきたのか、なぜそのカオスが「これや！」と思うほどおもしろいものなのか、先生は相手かまわずだんだん興に乗っていく。

パイこね変換。赤と青に色分けされたドットをパイ生地の粒子に見立て、生地を折りたたみ続けると、赤と青がだんだん混ざり紫色になっていく。隣り合う（＝初期値がとても似ている）粒子であっても、生地を折りたためば遠い場所へ混ざり合っていく。

　話が佳境に入っていくのは、リーとヨークがロバート・メイに出会ってカオス理論を世に発表するところだ。その顛末だけを手短かに紹介するが、この話は生態学の研究から始まった。最初は人口問題だ。
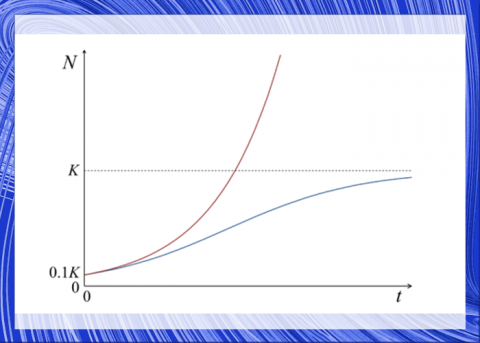
　世界の人口増加現象をめぐっては、古くから非線形の現象をどう扱うかということが問題になっていた。一番有名なのはマルサスの人口論である。マルサスは人口が幾何級数的（指数関数的）にふえるという見方をしていた。当時のヨーロッパでは人口増加は大社会問題で、へたをすれば食料危機がやってくるかもしれず、それなら産児制限や家族制度や移民のありかたを考えなおさなければならない。
　しかしマルサスのモデルは線形的だった。実際には人口はネズミ算的にふえるとはかぎらない。病死率の具合、飢饉の到来、疫病の流行、戦争による青年の減少、医療技術の変化など、多くの要因が絡む。人口問題はかなり複雑な現象なのである。
　ところが、これらを算段するような数学モデルがなかった。そこへピエール・ベルハルストのロジスティック方程式が登場して、非線形な現象を扱う可能性が出てきた。ロジ方程式は人口問題だけでなく昆虫の増殖や大腸菌の増加現象などにもあてはめられ、生態系の捕食と被食の関係を追ったロトカ＝ヴォルテラの微分方程式によるモデルなどに発展していった。
　山口先生にとって嬉しかったのは、京大の内田俊郎がゾウムシの個体数変化を研究してロジ方程式とは異なる差分方程式を導いたことだった。

　そんなことがあったのち、１９７３年にロバート・メイが物理学から数理生態学に転じて、これらの一連の研究の理論的背景を考察すると『複雑な生態系は安定性にはつながらない』という見解を示し、その特色が「きわめて複雑な軌道をもつカオティックなもの」だと形容した。メイはのちのイギリス学術協会の会長になっている。

ロバート・メイはシドニー出身のイギリス人物理学者であり数理生態学者。1973年にロジスティック式を利用して、生物の多様性と安定性の複雑性についての数値実験を行い、「複雑な生態系は不安定である」という当時の常識を打ち破った。後にもリーマン・ショックやCOVID-19など、差し迫るあらゆる社会問題に非線形の方法を応用した。

　ここで話がちょっと前後するのだが、乱流を研究していた気象学者のエドワード・ローレンツがストレンジ・アトラクター（いわゆるバタフライ型のローレンツ・アトラクター）を発見するという有名な出来事が入る。初期値に敏感な非線形のスターの登場だ。ただし、この有名な話は当時はほぼ誰も知ってはいない。
　ついでその成果に天啓のごとき刺激を受けたリーとヨークが漸近的な周期解をめぐる定理を確立して（これもアラン・ファラーがローレンツの論文コピーを二人に渡したからなのだが）、その論文のタイトルを「周期３はカオスを意味する」（Period Three Implies Chaos）としたまさにその前後（タイトルに「カオス」という言葉が使われたことも、当時はほぼ誰も知ってはいない）、二人にニューヨークで出会うことになるロバート・メイが「カオス」を世界中に認証させる気になったのだった。
　山口先生は、このカオス誕生のきわきわエピソードが大好きなのである。まるで人形浄瑠璃の道行までの経緯や菊田一夫のすれちがいのメロドラマのように再現したがるようなのだ。
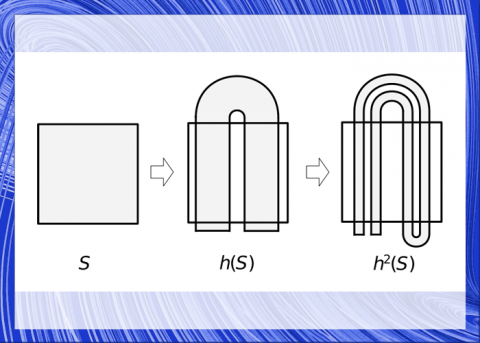
　本書はこのあとは、一次元離散力学系の周期軌道に関するシャルコフスキーの定理、京大の上田睆亮が組み立てた非線形振動の微分方程式（ダフィング方程式）、ポアンカレ（１８夜）のカオスの感覚を受け継いだスティーブン・スメールの位相幾何学っぽい馬蹄形力学などを紹介しながら、マンデルブロ集合とフラクタルな数学の案内をする。もちろん、このくだりも存分に堪能できる。

マルサスのモデルを適用した指数関数的増加曲線（赤）とロジスティック曲線（青）の比較。マルサスモデルは値の上昇に歯止めがかからないが、ロジスティック曲線は t → ∞に向かうにつれ、NがKに漸近していくことが確認できる。

ローレンツ方程式において初期値鋭敏性（バタフライ効果）があらわれる例。横軸は時間、縦軸はある変数の変化を示す。比較のための初期値は３つ用意している。水色は初期値 1.001、紫は 1.0001、朱色は 1.00001 である。時間が10を経過するまではほぼ同じ挙動だが、それ以降は全く異なった軌跡を描いている。

スティーブ・スメールは、難解な非線形振動の問題に対して馬蹄形力学という力学系のモデルを考案した。正方形Sの領域を伸ばして曲げてh(S)のように馬蹄形に変形し、元のSの領域に重ね写す変形を繰り返すことで、フラクタル構造をもつ複雑な写像となる。パイこね変換の力学系と同じく無限個の周期解が得られ、ある系が馬蹄形力学と同様の構造を持てばカオス的であるともいえる。

　それにしても、カオスの出現やカオスにまつわる研究の投企性は、どうして人々を興奮させるのだろうか。マダム・キュリーの奮闘やＤＮＡ二重らせんモデルの発見やフェルマーの最終定理（４３５夜）の氷解と同類のものなのか。どうも、そういうものとはかなりちがった感じがする。では、カオスには「これや！」と叫びたくなるどんな魅力があるのか。このことは研究者たちによって、充分には語られていない。ぼくの印象では、ジェイムズ・グリックが『カオス――新しい科学をつくる』（新潮文庫）というドキュメンタルに書いた一冊が人口に膾炙したからカオス・ブームがやってきたようなもので、残念ながら科学者たちによる興奮が広まったのではなかったのである。かつてボーアやハイゼンベルク（２２０夜）やシュレディンガー（１０４３夜）やド・ブロイ（３４９夜）が量子力学の興奮と苦悩を、それぞれの問題意識と文体で書きつづけたことにくらべて、カオス研究の熱度はあまりにストイックすぎるままなのだ。
　それにカオス理論はそうとうに難解なので、いっとき興奮してもすぐにさめる連中も多く、文化系からはともかく、理科系からの考察がまったく持続していないようにも思われる。数学系からの啓蒙も、たとえばホフスタッターの『メタマジック・ゲーム』（白揚社）などの凝った工夫もあったけれど、総じては生真面目すぎる大学生相手に終始したままだ。山口昌哉はなかなかいないのだ。

　本書の最終章に、山口は九鬼周造（６８９夜）の『偶然性の問題』を引いて、九鬼が必然性は「存在がそれ自身に根拠をもつ場合」だが、そうでない存在もあって、その存在が偶然なのであると言い、それなのに確率論も量子力学も偶然そのものを扱っていない。多くの学問は必然性ばかりに自分の身を寄せている。形而上学だけが偶然に学問的に迫れるだけじゃないかという言い分をあげて、こんな感想を綴っていた。ちょっと紹介しておく。
　カオス研究が偶然性そのものの研究になってはまずいけれど、カオスを研究することは、偶然性が必然性へと近づく場面を必然性の側から眺めているともいうべきかもしれない、と。
　また生物学や物理学がカオスに向かうにあたっては、生物が外部環境からのゆらぎに対応するために自律的なゆらぎ（カオス）を派生させているのではないかというような見方、生物がつくりだすカオスは特有の生物言語の文法をもっているのではないかという見方、物理的なカオスの研究は化学振動との関係や非線形光学との関係を追ってみるという見方、そんなことがあってもいいのではないか、と。
　もっともっと洩しておいてほしかったけれど、とくに文法をもつ生物カオスなどのアイディアは誰かに継承して起爆してもらいたいところで、そこに先生がさらに特異なヒントをかぶせてもらえるといいのだが、残念ながら１９９８年のクリスマス・イブに７３歳で亡くなった。

共振器のなかの光線軌道（図a）とシミュレーションによる光の強度分布図（図b）。実験結果と計算結果が一致していることがわかる（図c）。非線形な軌道を示す光線は、通常の電磁場では考えられない現象をあらわすため、その発生や制御の条件が研究されている。

　ところで、山口昌哉の健気でやんちゃな自在感がそこそこ躍如している本が、もう一冊あった。『無限・カオス・ゆらぎ』（培風館）という本で、全ページが座談会記録なのである。サブタイトルは「物理と数学のはざまから」、座談をしているのは、寺本英、広田良吾、武者利光、山口昌哉だ。１９８５年の刊行だから、本書のちょっと前。先生、このころ絶好調だったのだろう。
　よくぞこんな企画が生まれたなと思ったが、山口が武者の『ゆらぎの世界』（講談社ブルーバックス）をおもしろく読んだので、寺本さんにも読んでもらったところ、うんうんいい線だということになり、それならみんなで「無限と有限」や「離散と連続」や「デジタルとアナログ」について忌憚なく喋り合おうかということになったようだ。それを培風館があまり手を入れずに本にしたので、山口だけでなく、全員の好みや迷いや跳びが出ていて、たいへん愉しい一冊になった。
　この手の本、もっとあるといいのだが、最近はとんと見当たらなくなった。科学や数学がコンプライアンスしたら、もうおわりなのに、みんなじっと何かに耐えているようで、息苦しいかぎりである。

『無限・カオス・ゆらぎ』（培風館）。独自の文化圏をもつが、４人の物理学者・数学者が一堂に会して分野をまたいだディスカッションを行う。討論の冒頭で、山口昌哉は物理学と数学の使命のちがいについて、「物理学は真実を追求するが、数学は物の見え方を研究している」という意見を投げかけている。

いろいろフラクタル図形①
フラクタルな図形が円の外側にむかって無限小にいたるように連続的に描かれた、エッシャーの『サークルリミット』。外側の図形は小さく見えるが、双曲幾何の世界では全て同じ大きさである。このフラクタル図形と志村-谷山予想のつながりが、フェルマーの最終定理を解く鍵になっていった。

いろいろフラクタル図形②
木の枝にはさらに短い枝が生えている。身近な樹木にもフラクタルは潜んでいた。ここで試しに図aのカラー画像を白黒にし（図b）、枝葉部分だけを切り出したうえで（図c）輪郭線を強調する（図d）。すると大陸のような模様が浮かび上がる。じつは入り組んだ海岸線にもフラクタル構造は確認されている。さらに、背景色を反転し木漏れ日を復元すれば、また別様のフラクタルが浮かんでくる。

いろいろフラクタル図形③
無数の水や空気の粒が揺れ動く中で生まれては消えるゆらぎの現象を、発見者にちなんで「ブラウン運動」という。この軌跡も部分と全体が響きあっている。図はブラウン運動の方程式を用いて、揺れる水面やたなびく雲のような流体模様を再現したもの。

いろいろフラクタル図形④
マンデルブロ集合（左図）は、細部を拡大するといたるところに全体と同じシルエットを発見できる。金剛界曼荼羅（右図）もまた、曼荼羅を要素に持つ曼荼羅である。どちらも世界の構成単位に世界全体が写されるホロニックな自己相似性を内包している。

いろいろフラクタル図形⑤
カントール集合とは、長さ１の線分（───）を３等分して真ん中を取り除き（─　─）、新たにあらわれた線分に同様の操作を無限に繰り返すことで得られる集合である。図版は、立方体を27等分して8角の立方体のみ残す操作を無限に繰り返して得られる集合のカントールの塵である。どれだけ部分を拡大しても全体と同じ形になる自己相似形が表れるためフラクタルである。

TOPページデザイン：富山庄太郎
図版構成：寺平賢司・梅澤光由・大泉健太郎
中尾行宏・桑田惇平・齊藤彬人

⊕『カオスとフラクタル』⊕
∈ 著者：山口昌哉
∈ 編集：大江千尋
∈ 協力：宇敷重広
∈ 装幀：（文庫）安野光雅
∈ 発行者：喜入冬子
∈ 発行所：株式会社筑摩書房
∈ 印刷：株式会社精興舎
∈ 製本：積信堂
∈ 発行：2010年

⊕ 目次情報 ⊕
∈∈ はしがき
∈ 第１章　非線形とは何か
∈ 第２章　個体群生態学での非線形とカオスの発見
∈ 第３章　カオスの物理・カオスの数理
∈ 第４章　工学および数値解析とカオス
∈ 第５章　カオスからフラクタルへ
∈ 第６章　カオスとフラクタル―今後の展望
∈∈ 参考文献
∈∈ あとがき
∈∈ 解説「カオスとフラクタル」今昔（合原一幸）
∈∈ 索引

⊕ 著者略歴 ⊕
山口昌哉（やまぐち・まさや）
1925〜1998年。京都生まれ。京都大学数学科卒業。京都大学工学部教授、理学部教授、理学部長をへて同大学名誉教授。理学博士。専攻は非線形数学、非線形偏微分方程式の数値解析。生物科学や社会科学への応用にも関心が深かった。著書に『非線形現象の数学』『カオス入門』（ともに朝倉書店）他。