Pauca sed Matura・・・。
赤堤通りの３階建ての一棟に編集工学所が引っ越しする直前のことだ。１階の天高４メートルのスペース「本楼」の内装があらかた仕上がったあと、本棚劇場の向かって右側のネステナーの黒い鉄板にライトグリーンのエナメルで、こういうラテン語の箴言を書いて掲げた。「少数なれど、熟したり」と訳している。
ガウスが印象に彫った座右銘だ。向かって左側には、同じくエナメルで老子の言葉の英訳を書いた。「上善、水の如し」にまつわる一節だ。書体は美柑和俊君に選んでもらった。
Pauca sed Matula・・・。ガウスがこのラテン語を座右銘に選んだ経緯は伝わっていないが、まことにガウスらしいとも、ガウスにしてこのモットーだったのかとも思わせる。数学史家たちは、ガウスはつねに完全主義をめざしていたので、どんな科学的発見や数学的到達も多くの者が理解するところとは異なるものになっているかもしれないが、ガウス本人はそれが少数にしか理解できないものでも完璧に熟していると確信していたという意図を表明したのだろうと、あるいはまた、自分は少ししか論文を発表していないけれど、それでもそのすべては十全に熟しきったものであるはずだと自負していたと、解釈している。
もっともらしい解釈だが、ぼくはこれらの説を採らない。ガウスは、科学や数学の提示というものはぶっちぎりにならざるをえないと思っていたはずなのである。仮にガウスが慎重な詰めに徹していた数学者だったとしても、少数者になることを怖れないという意志を表明したかったのだろうと思う。編集工学研究所には、この意図を掲げておきたかったのだ。
豪徳寺・本楼の舞台「本棚劇場」の天井桟敷にある黒板壁面には、松岡のモットーが掲げられている。左には「The mighty and great will be laid low;The humble and weak will be exaltedーLao Tzu」（強大なるは下にあり、柔弱なるは上にある―老子）、右には「Pauca sed Matura」(少数なれど熟したり―ガウス)。
ガウスによって科学界と数学界にもたらされた成果が広域にわたっていたこと、そのいずれもが先駆的であったこと、その先見の明が卓抜きわまりないものであったことは、いまでは押しも押されぬものになっている。
ガウス関数、磁束密度単位ガウス、ガウス分布、ガウス・クリューゲル図法、ガウス曲率、ガウスの発散定理、ガウス平面、ガウス和、小惑星ガウシアなど、ガウスの名を冠した数学用語や測定用語も数十に及ぶ。しかし、ガウスの実像はあまり詳しく語られてこなかった。
ダニングトンはこの本を仕上げるのに、なんと３０年をかけた。一人の伝記に費やした年月としてはそうとうに長い。ガウスが偉大すぎていたからとか評価が定まらないからだとかのせいではなく、また評伝の構成に凝ったからというのではなく、史料の総点検に著者が単身で向かったからだろう。おかげで申し分ないガウス像が手に入るようになった。いまも本書に勝る評伝はない。
そうではあるのだが、あいかわらずというか、少数者であることを怖れなかったガウスの自業自得というべきか、ガウスを痛快に語るという空気がいまもって伝わってこないのである。ガウスはゲーテ（９７０夜）やバルザック（１５６８夜）のようには語られず、プルースト（９３５夜）やモネやボブ・ディランのようには好まれなかったのだ。ガウスを勢いよく語ったのは、日本人ではひょっとして高木貞治（５４夜）だけだったのではないかという気がする。これでは困るのだ。
なぜガウスは語りにくいのだろうか。おそらく円熟しきった数学者のように感じられるからだろうが、そんなことはない。本書ほど詳しい評伝からは、ガウスが時期ごとに、事態ごとにいかに危ういコースを歩んできたのか、よくよく伝わってくるはずだ。
名が刻まれている①・・・ガウス分布・ガウス関数
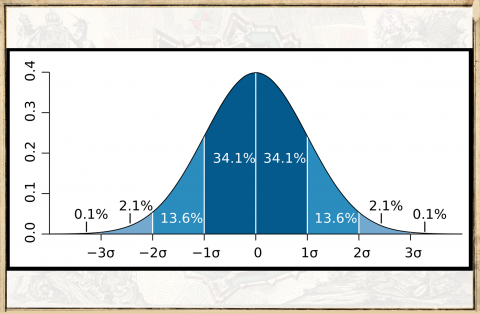
ガウスは、天文学の観測データにみられる測定誤差の性質を求めた。「ガウス分布」は、ある出来事の観測データが、図のように平均値の付近に集まる釣鐘状の分布になることを示し、「ガウス関数」は観測データの値が発生する確率を面積として計算することを可能にする。
名が刻まれている②・・・磁束密度単位ガウス
ガウスは、糸につるした棒磁石が地磁気の影響によって振動する様子を望遠鏡で観測し、そのデータを数学的に処理することで精密な結果を得られるようにして、この領域の発展に貢献した。ガウス没後のパリの国際電気会議で、磁束密度の単位にガウスの名が与えられた。
名が刻まれている③・・・ガウス曲率
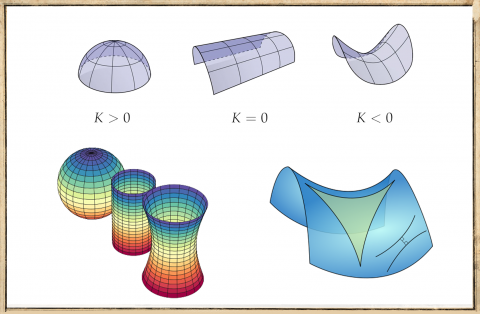
ガウスはユークリッド幾何学の平行線公理を否定する幾何学の探求にむかっていた。曲面の曲がり具合をあらわす曲率を使って、曲面を球面に写像するガウス写像や、最大の曲率と最小の曲率をかけて得るガウス曲率（K）をあみだした。Kの値が正、ゼロ、負の値をとるとき、図版上のような曲面の形状となる。図形に対応させると図版左下のように、Kが正なら球、Kがゼロなら円柱、Kが負なら双曲面となる。双曲面では図版右下のように三角形の内角の和が180度より小さくなり、球では180度より大きくなる。
名が刻まれている④・・・ガウス平面（複素平面）
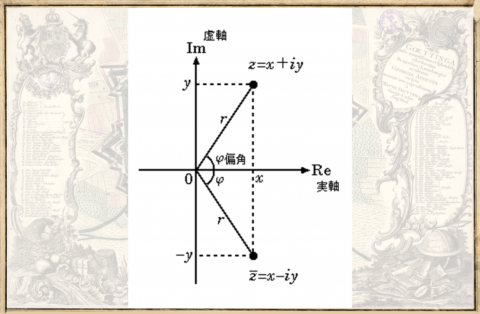
ガウスは、2つの実数（有理数と無理数の集まり）と虚数単位iであらわされる複素数（z=x+iy）を、実軸と虚軸をもつ平面に対応づけた。このガウス平面というツールを用いて、正十七角形をあらわす方程式を代数的に解くことにより（四則演算と累乗根の有限回の組み合わせで解を表現）、作図可能な条件を満たすことを示した。
ぼくがガウスに託しているものは２０代後半からほぼ変わらない。１７世紀前半のピエール・ガッサンディから１９世紀半ばのガウスに及んだ科学哲学的自然観をよりすぐって凝縮して、松岡正剛ふうの編集思想のレシピにしたまま大切な編集料理につかってきたからだ。
ガッサンディは、プロヴァンスの大学で神学と哲学を教えながら言語学と数学に秀でた発想をした碩学で、ラテン世界にギリシア自然学がもちこまれて以来、エピクロスが過小評価されていることを断ち切り、返す刀でデカルトに文句をつけ、時間と場所は天地創造以前からの物質の運動によって開始していたことを宣言した男である。
その、反デカルト・親エピクロス・ガリレイ派であるガッサンディの「物質の自然学」に端を発して、望遠鏡や顕微鏡の製作に携わった面々の勇気と、それらを覗いて自然の秘密に挑もうとした何人かのレンズ・フェティッシュたちの観測と思索を通した自然学のセンスが、球面収差と色収差の問題に解決の緒を与えたスイスのレオンハルト・オイラーの数学に及び、これらのいっさいを引き連れたフリードリッヒ・ガウスの数々の挑戦に「全自然学に向かった構想」を感じてからというもの、ぼくはガウスをもとにいっさいの編集思想の基礎工事にとりくみたいと考えるようになったのである。
基礎工事はけっこう大変だった。ぼくのような考え方を採る科学史家や思想史家が驚くほど少なかったからだ。
たとえばフランツ・ボルケナウに大著『封建的世界像から市民的世界像へ』(みすず書房)があって、そこにはデカルトやパスカル（７６２夜）と並んでガッサンディについても一章があてられているのだが、その解釈がデカルトに寄りすぎていて、つまらない。そのため、いちいち読み替えをしながら進むわけで、そんなことをしているとそのうち巨きなクロニクルを独創せざるをえなくなり、そういう作業にも精力を投下しなければならなくなるのである。それでやっとガッサンディの位置を修正したとなると、今度はその修正ガッサンディを誰が受け止められたのかを点検しなければならなくなる。修正ガッサンディは「エピクロス＝ガッサンディ」ということだから、ここからは唯物論や原子論の思想の変転まで視野に入れた大点検が必要になる。
そうなると、ぼくの勘だけでは危ない。若い時期に湯川秀樹さんのところにしばしばお邪魔していたのは、この勘を最強の言葉で補強してもらうためで、大いにコーチングをしてもらってなんとか乗り切れた。
とはいえ湯川さんのヒントにはぶっとんだものも含まれていて、「あんた、ガッサンディをやるんやったら、ボスコヴィッチも大事やで」というものだから、その夜からは一ヶ月以上をかけて原書の入手さえおぼつかないボスコヴィッチに没頭するわけなのだ。ボスコヴィッチはラグーサ共和国（クロアチア）のイエズス会士で、ニュートン力学を大陸側で理解した最初の一人であるとともに、物質の力を均一な原子の運動として理解しようとした最初の自然哲学者であって、いわば原子論の先覚者なのである。
それで、またまた湯川さんを訪れてこれこれしかじかで凄いことになりますね、これってガウスにまで及びますか、量子力学まで及びますかとお伺いをたてると、そこはあんたの裁量や、思い切っていきなさいなのだ。
こんなふうでは、それまでのクロニクルやマッピングがまたまた大修正を迫られる。おまけにガッサンディとボスコヴィッチをつなげて語る科学者など、湯川さん以外にはほとんどいない。そこからオイラーやガウスを引き取るとなると、もはやそんな議論はひたすら孤立無援なのである。
まあ、こんな調子だったのである。もっとも、こうしたことはいまだに若気の至りとは思っていないことなので、今夜はそのことを記してガウス案内に代えてみたいと思う。
ぼくの最初の単行本は『自然学曼陀羅』（工作舎 １９７９）である。「遊」創刊号から連載していた同名のエッセイをまとめ、そこに二、三の付録をくっつけたものなのだが、これはいわばガウス型の自然学解明の方法に対するぼくなりの偏愛を訴えたマニフェストだった。タイトルは「自然学」がさまざまな科学の愉快を統合する方面を、「曼陀羅」が精神や文化の跳ね返りを引き受けている方面をあらわしていた。
読んでもらえばわかるように、冒頭９ページに早々とガッサンディが出てくる。それが数ページ進むとレンズ・フェティッシュたちの話になって、オイラーにつながっていく。そのあとアルハゼンの『光学宝典』と「薄明論」に寄り道をして、イスラム科学による冒険を少しとりあげたのち、いよいよガウスが登場し、以降は何度かガウスを縫いながら全自然学構想をスケッチしていくというふうになる。
「遊」9号『存在と精神の系譜』のガウスの項では、「曲率概念の司祭、光に憑かれた自然哲学者、電磁気と格闘する男、誤差の論理哲学者」の4人のガウスが登場する。4人のガウスが束となることで、自然を写像した従来の数学から、概念そのものが動き出す世界観＝全自然学構想が打ち立てられる。ガウスによって数学は、自然の似姿を映し取る道具から、道具が自立して相互に関係しあい構造化されるもう一つの世界へと再構成されていったのである。
ガッサンディも、ボスコヴィッチも、デカルトが拠って立つ力学的世界像を批判した。形や大きさ、絶対的自己同一性を保持するハードな原子を前提にした完全無欠の世界像ではなく、原子自身の誤りや逸脱も包摂する世界像を構想した。ガッサンディは言うまでもなく、ボスコヴィッチにもエピクロスの「偏倚原子説」に由来するような原子イメージがあった。湯川秀樹は、現代物理学を予見していたかのようなボスコヴィッチの「加速する点粒子の仮説」についての先駆説を重視した。
松岡の初期の著書『自然学曼荼羅』（工作舎）。銀色の特殊紙のカバーに白のオペークインクで刷られた。デザインは木村久美子。『自然学曼荼羅』に収録された付録「ガウスー彗星と重力」は、「素粒子は存在と運動の片方しか捕捉できない」という原理からはじまる。この奇妙な事実は、視覚と対象が相互的だからではなく、対象の構造が相対的な運動関係にあるため起きる。この原理はガウスの彗星軌道計算に類比された回転扉によって覆される。本書ではまた、ガウスが構造化した全自然学構想とマルセル・デュシャンの《１落ちる水、２照明用ガスが与えられれば》がダブルページに置かれ、知覚されえない重力という現象が自立したもう一つの世界の中に立ち現れてくることを示唆する。
さて、ぼくのお気にいりのガウスの最初のクライマックスは、大学時代に定規とコンパスだけで正十七角形を作図したことだ。それまで作図できる正素数角形は正三角形と正五角形だけだと思われていたのに、２０００年ぶりに新たな可能性が出現したのである。
数学界が仰天した。晩年のガウスは墓標に正十七角形を刻んでほしいと願ったようだが、後塵たちは墓標ではなく記念碑をつくってそこに正十七角形をあしらった。これはガウス的ではなかったのだが、まあ、そんなことはどうでもいい（実はどうでもいいわけではないのだが、今夜のところはお目こぼしだ）。
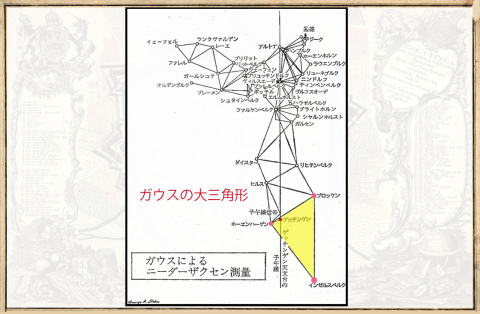
次のクライマックスは少しとんで、ガウスが弟子たちとブロッケン山に登って準備怠りなく夜を待ち、三つの山の頂上でカンテラのシェードを開けて「光線の三角形」をつくりだし、その内角の和を測定することで、そこに非ユークリッド幾何学の不安定数を確認しようとしたあの夜の出来事の前後である。
不安定数とは曲率のことをいう。１８２５年前後、ガウスは『曲面に関する一般的考察』を書いて、屈曲はできても伸縮できない面をどのように変形させようとしても、曲面上の各点における主曲率の和は変わらないという定理を説明してみせた。
一方、ガウスはユークリッドの第５公準「平行線は交わらない」を訝っていた。すでに似たような疑問をもつ科学者や数学者たちもいた。なかでもボヤイ父子と親しくなった時期、ガウスは第5公準で自然界を語ろうとしてきたのは根本的な過誤ではなかったかと思うようになり、ひそかに非ユークリッド三角法を工夫していた。こうしたことが重なってきて、その問題の分岐点にある問題を実地に確かめたくて、ブロッケン山で光線三角形の角度測定に挑もうとしたのだった。
むろんそんな程度の高さの山では、いくら精密に測ったところで内角の和は１８０度を上回りも下回りもしない。実験は失敗したのだが、ガウスはそんなことにこだわってはいない。猛然と非ユークリッド幾何学が成り立つような世界について、さまざまな思索と試算を試みていった。
実際にはどんな思索と試算をしていたのか、本書『ガウスの生涯』もあれこれの断片を集めて想像しているが、はっきりしたことはわからない。ぼくは勝手に、のちのちアインシュタインが「空間は物質の詰まりぐあいの曲率で決まる」とみなしたような、すこぶる相対的な時空間を思い浮かべていたのではないかと臆測したいのだが、まあ、これは言い過ぎだろう。
正十七角形を作図する様子。ガウスは作図の手法を円分体の理論として体系化し、『整数論の研究(原題: Disquisitiones Arithmeticae)』の第七章で論じた。その中で正十七角形のみならず、一般の正多角形に対しても定規とコンパスによって作図できる条件を与えている。
ガウスは長距離の三角測量を可能にするために、100ｋｍ以上離れた場所でも名刺大の鏡が１等星の明るさで見える回照器（ヘリオトロープ）を考案していた。回照器が完成するまで、六分儀に鏡をつけたものを三脚に乗せ、副回照器と呼んで使用した。この装置がドイツの旧10マルク紙幣の裏に描かれている。
1807年から1855年に亡くなるまで、48年間ゲッチンゲン天文台の台長を務めていたガウスは、ゲッチンゲン天文台を通る子午線を三角測量網の経度の基準にしようと考えていた。ガウスが測定した、ゲッティンゲン近郊のホーエンハーゲン、ハルツ山脈のブロッケン、南のテューリンガーヴァルトのインゼルベルクを結んだ図形は、ガウスの大三角形と呼ばれている。
ガウスについての三つ目のクライマックスは、クライマックスとしてはわかりにくいかもしれないが、アレクサンダー・フォン・フンボルトとの包摂的な交際の中に認めたい。このことについても本書はほとんどエビデンスを並べられずにおわっていたが、しかし、ガウスがフンボルトの巨視的な思考力と交わっていたことは、ガウスの全自然学構想とかなり共振できたはずだった。
アレクサンダーの兄が言語学者のヴィルヘルム・フォン・フンボルトである。弟のフンボルトは博物学者で、鉱山学の専門でもあった。鉱山学はしばしば結晶学に熱中していたガウスにも親しいもので、おそらく二人はその手の話題を何度も交わしたはずである(フンボルトがガウス家の賓客として何度か滞在したことはわかっている)。
しかしぼくが想像するのは、フンボルトがやがて著作することになる『コスモス』の内容をガウスと交わしたであろうということだ。『コスモス』はフランスではボードレール（７７３夜）が絶賛し、アメリカではエドカー・アラン・ポー（９７２夜）が換骨奪胎して『ユーレカ』にまとめなおしたものだ。ガウスがこの内容を知らなかったはずはなく、知っていたならガウスの自然学と溶け合っていったはずなのである。
ガウスは１８５５年に７７歳で亡くなっている。晩年の１０年間は「少数なれど熟したり」の仕上げのコーダだ。このことをガウスは大いに満喫した。その全容に『コスモス』のファンファーレが鳴り続けていたのである。
ところで、『自然学曼陀羅』には１８４５年から１８５５年までの瞠目すべき略年表が載っている。その一部をここに再掲するが、この出来事のうねりこそ、実はガウスの全自然学のうねりそのものなのではないかと思われる。こういうものだ。
１８４５ ファラデー効果の発見
フンボルト『コスモス』
マルクス『ドイツ・イデオロギー』
デュマ『モンテ＝クリスト伯』
ワーグナー『ローエングリン』
１８４６ 海王星の発見
ベルナールの実験医学開始
光学機器会社カールツァイス設立
リーマン、ガウスのもとで学ぶ
ホーによる輪転印刷の開始
１８４７ ヘルムホルツのエネルギー恒存則
ブール「論理の数学的分析」
エミリー・ブロンテ『嵐が丘』
１８４８ パスツールによる光学異性体の発見
フランス2月革命
マルクス＝エンゲルス『共産党宣言』
ポー『ユーレカ』
ワーグナー『ニーベルンゲンの指環』
ラファエル前派結成
ディケンズ『デヴィッド・コパフィールド』
１８４９ キルヒホフの法則
フィゾーによる光速度測定
ガウスを祝う黄金祝賀祭
ラスキン『建築の七燈』
佐久間象山の電信実験
キルケゴール『死に至る病気』
１８５０ クラウジウスの熱力学第二法則
プリチャードによる天体観測写真法の提案
デデキントがガウスのもとで学ぶ
ホーソン『緋文字』
１８５１ ロンドン万国博覧会
リーマン「複素関数論」
フーコーの振子による地球自転速度の測定
英仏間に海底電線
メルヴィル『白鯨』
１８５２ グリム兄弟『ドイツ語辞典』第一巻
アンリ・ジュフールによる最初の飛行船
１８５３ ハミルトン「四元法講義」
ケルヴィンによる放電の周期性の発見
日本に黒船来航
１８５４ リーマン「幾何学仮説」
クリミヤ戦争でナイチンゲール勤務
１８５５ リサージュの振動図形論
２月２３日、ガウス死去
パリ万国博覧会
ボードレール『悪の華』執筆中
ざっとこういうものだ。とくに恣意的に略年表化したわけではないが、それなのに、ここにはすべてが響鳴しているような交響力を感じる。ガウスが生きた時代が格別なのである。多くの識者や表現者が「全容」というものに向かえたのである。
フンボルトはそのシンボルの一人だった。ガウスもその全容に向かった一人だった。よきかな、よきかな、ナポレオンの野望と大失敗。よきかな、よきかな、ゲッティンゲンの少数なれど、熟したり。
ガウスの生きた時代①・・・文知の白鯨・分知の万博
メルヴィルの『白鯨』は文学の名を借りた海洋・博物百科事典。おびただしい「文知」を網羅し物語を融合させる方法文学のスタイルは、東西の博物的オブジェを蒐集し植民地主義的観点によって分類した万国博覧会の「分知」とも対峙する。
ガウスの生きた時代②・・・ホーの輪転印刷機・ポーのユリイカ
リチャード・マーチ・ホーは輪転印刷機による高速印刷技術を発明しグーテンベルク以来の技術革命を起こし活字による情報爆発のトリガーを引いた。エドガー・アラン・ポーは『ユリイカ』（ボードレールによるフランス語訳初版）の中で、宇宙は一点の統一より放射され拡散し引力と斥力の膨張と収縮にあるという直観の宇宙論を散文詩に書いた。
ガウスの生きた時代③・・・塵のラスキン・光のファラデー
近代化の進む英国ヴィクトリア朝では複製品が横行し、ハンドメイドのざらざらとした質感が失われていった。ラスキンは時代に背を向け、ゴシック建築に潜む記憶や塵の思索によって、本来の倫理を見出そうとする。英国王立協会に在籍したファラデーは、青少年へのクリスマスの贈りものとして、何種類ものロウソクを使った実験を披露した。ロウソクの片りんから宇宙を覗かせ、科学の行方を照らしだしたのだ。
ガウスの生きた時代④・・・瞠目の通信網・項目の博物学
19世紀になると、人類の情熱は増殖しつづける粘菌のように全自然学へむかった。フンボルトは、地理学の大著『コスモス』を書き、ブレッド兄弟が敷設した海底ケーブルは、わずか50年で世界を覆った。
ガウスの生きた時代⑤・・・予見から海王星・事件からディケンズ
海王星は、ニュートンの万有引力では説明できない天王星の軌道のズレを説明しようとしたルヴァリエが、存在を予見し、その後ベルリン天文台でガレとダレストによって実在が確認された。ジャーナリストだったディケンズは、事件の全容をあまねく説明せずとも、読者に事態を追体験したと錯覚させたかった。やがて、幼い子供の視点を通した文体や人物描写に手ごたえを得ていく。天文学は見える星によって未知の星の存在を探り、文学は描かれない事態によって事件を描く。
TOPページデザイン：松田行正
図版構成：寺平賢司・梅澤光由・大泉健太郎
中尾行宏・桑田惇平・齊藤彬人
⊕『科学の王者 ガウスの生涯』⊕
∈ 著者：ダニングトン
∈ 訳者：銀林浩, 小島穀男, 田中勇
∈ 編集：大竹進、外間敬子
∈ 装幀：戸田ツトム
∈ 発行者：ー
∈ 発行所：東京図書株式会社
∈ 印刷：ー
∈ 製本：ー
∈ 発行：1976年
⊕ 目次情報 ⊕
∈∈ まえがき
∈∈ １ 序章 血族的背景
∈∈ ２ 魅惑的な少年時代
∈∈ ３ 学生時代
∈∈ ４ 青年ガウス
∈∈ ５ 天文学と結婚と
∈∈ ６ その後の活動
∈∈ ７ 再びゲッチンゲンへ
∈∈ ８ 労苦と悲しみ
∈∈ ９ 若き教授-発見の10年間
∈∈ １０ 測地学に明け暮れ-過渡期の10年間
∈∈ １１ ヴェーバーとの連携-激動の年
∈∈ １２ 電磁気学で電信機の発明
∈∈ １３ 磁気-物理学に専念
∈∈ １４ 曲面論、結晶学、光学
∈∈ １５ 非ユークリッド幾何学の萌芽
∈∈ １６ 試練と勝利-紛争の体験
∈∈ １７ 大道や間道での道標
∈∈ １８ すばらしい老年
∈∈ １９ ヨーロッパ数学界に君臨
∈∈ ２０ ドイツ科学界の長老
∈∈ ２１ もろもろの糸をたぐって広大な地平へ
∈∈ ２２ 科学と宗教-真理を愛する哲学者の信仰宣言
∈∈ ２３ 日没、黄昏-隠棲
∈∈ ２４ エピローグ
∈ 一 列聖 エヴァルトとザルトリウスの弔辞
∈ 二 招魂の廟堂 歿後の顕章と栄誉
∈∈ 年譜
∈∈ 注
∈∈ あとがき
⊕ 著者略歴 ⊕
G・ウォルド・ダニングトン（Dunnington, Guy Waldo）
1906年ミズーリ州ボウリンググリーン生まれ。作家、歴史家。ドイツ語教授。彼の小学校の教師の一人がガウスのひ孫であったことがガウスに興味を持つきっかけとなった。ガウス関連資料のコレクションを所蔵しており、この種のコレクションとしては世界最大と考えられている。著書は本書『Carl Friedrich Gauss: Titan Of Science 』（Hafner、1955）がある。
⊕ 訳者略歴 ⊕
銀林浩（ぎんばやし・こう）
1927年、東京生まれ。東京大学理学部数学科卒業。明治大学名誉教授。遠山啓とともに「水道方式」と呼ばれる算数の指導方法を提唱し、自らも数学教育協議会委員長として普及に努めた。著書に『量の世界：構造主義的分析』（麦書房）、『水道方式による計算体系』（遠山啓との共著、明治図書出版）など、訳書にベル『数学をつくった人びと』（共訳、ハヤカワ文庫）、コクセター『幾何学入門』（ちくま学芸文庫）などがある。
小島穀男（こじま・のぶお）
1940年、東京大学工学部船舶工学科卒業。三菱重工業株式会社技術本部顧問を務めた。
田中勇（たなか・いさみ）
1954年、青山学院大学文学部卒業。法政大学大学院社会科学研究科政治学専攻博士課程修了（出版時）。著書に『アメリカの現代史』（講談社、1970）、訳書にマーチン・ガードナー編『サム・ロイドのパズル百科』（白揚社、1967）、E・T・ベル『数学をつくった人びと』（銀林浩と共訳、東京図書、1976）などがある。
