数学的思考

人間の心と学び

デービッド・トール

共立出版 2016

David Tall
How Humans Learn to Think Mathematically : Exploring the Three Worlds of Mathematics 2013
編集：大越隆道　監訳：磯田正美・岸本忠之　訳：添田佳伸・木根主税・渡辺耕三ほか

アサト	校長、おめでとうございます。
校長	やあ、十装ダリア、久しぶり。おめでとう。
イーディ	異次元イーディです。あけましておめでとうございます。１月５日に全身麻酔の検査をされたと聞きましたが、体調はいかがですか。
校長	あいかわらず青息吐息。桃色吐息にしたい（笑）。
アサト	いろいろもっと教えていただきたいので、これからもお元気でいてください。
校長	うん、なんとかね。今月末で７９歳だけどね。で、今日はなぜ二人が揃ってるの？　３７花の花伝所の師範と入伝生だったんだよね。
アサト	イーディはその後は「守」の師範代です。
イーディ	いま「守」をやってます。
校長	知ってるよ。花伝所の話？
イーディ	いえ、新年早々の突然「寿」インタヴューです。
校長	そりゃめでたい。獅子舞だな。何についてのインタヴュー？
イーディ	校長はしばしば数学を話題にしてこられてきましたよね。
アサト	小坂別当方師が紹介されてましたが、「遊」の創刊号で「エルランゲン・プログラム事件」を書かれていた。フェリックス・クラインですよね。聞けば、最初に対外的な執筆原稿を書いたのが「１７歳のための幾何学」だったそうですね。
校長	うん、非ユークリッド幾何学についてのね。２５、６歳のときに高校生に向けて書いた。
イーディ	それで新春を寿いでお聞きしたいのは、数学って編集工学にとってはどういうものだと見ているのかということです。松岡正剛にとって数学って何かということを伺いたいんです。それからもうひとつ、新年最初の千夜千冊にぜひ数学本をとりあげていただきたくて、やってきました。
校長	まさに脱兎なおねだりだねえ。そうか、イーディは中学生に数学を教えているし、アサトは根っからの数学派で、行列式の専門だもんね。ぼくの数学思想ねえ。そうだなあ、一言でいえばアンリ・ポアンカレ（１８夜）が言っていることに準じてきたかな。
イーディ	ポアンカレ？　トポロジーの？
校長	トポロジーもだけど、それより『科学と方法』や『科学と仮説』（岩波文庫）のポアンカレです。ほらポアンカレは「数学とは、異なるものを同じものとみなす技術である」と言ったでしょう。まさにそれです。技術と訳したけれど、もとはアートだからこれはＡＲＳで、ラテンっぽくいえば、数学は「さまざまな異同をまたぐアルス・マグナだ」ということになるよね。ぼくの数学観はほぼここにあります。この出発点は編集工学と同じです。
イーディ	「異なるものを同じものとみなすための技芸」ですか。はい、カッコいいですね。まさにその通りです。伺ってスッとしました。
アサト	数学も編集も一貫して、そこですよね。ぼくは最近、編集工学を圏論（category theory）で見るようになったんですよ。
校長	ほうほう圏論ね。おもしろい。斎藤毅？　ＭＴ数学？
アサト	斎藤さんの『数学原論』（東京大学出版会）やＭＴ数学のユーチューブまでご覧になっているんですか。
校長	まあね。最近の若い数学派は発想がおもしろいね。長浜バイオ大学の西郷甲矢人（はやと）くんの『圏論の地平線』（技術評論社）なんかもね。長浜はぼくの原郷です。それで圏論と編集の関係？

エルランゲン大学就任時、数学者クラインは後にエルランゲン・プログラムと称される小さな論文を発表する。当時多方面に分化していた種々の幾何学を統合する画期的な方法が書かれていた。松岡がこの幾何学の方法を直感や観念に適用したところ、今このようにしてモノゴトを考えている脳や意識までも、変換の幾何学として捉えられるという驚くべき結論が導出された。この「脳のトポロジー」とも言える導出過程をまとめた39箇条は『エルランゲン・プログラム事件』と名付けられた。
「遊」創刊号より

アンリ・ポワンカレは、19世紀のフランスの数学者で、非ユークリッド幾何のポアンカレのモデルを発見した（上）。非ユークリッド幾何学の発見によって、幾何学は図形を扱う具象的な学問から、抽象的な分野へ領域を広げた。下の図は双曲幾何学のモデルで、ポワンカレ円盤と呼ばれるもの。

「MT数学」は、数学や数学史などについて発信しているYoutubeチャンネル。臨刊アフロール教室の師範代のように、かわいらしい被り物をしながら、難解な数学のイシューを次々に解説している。

アサト	編集ってさまざまな情報の束を結び付けていくわけですよね。結び付けていって、そこに成立するさまざまな群や層や圏や束を並立させていく。圏論もさまざまな情報対象を「射」（morphism）でいろいろつないでいきますね。複数の対象を矢印（arrow）でつなげていくと、何本もの「射」の関係軌跡が「圏」（category）をつくります。そのできあがった圏を束ねていくと、そこに射の型のようなものが見えてくる。これは「型射」ともいうべきモルフィズムですよね。
校長	準同型めいたものが揃ってくるからね。おまけに圏論ではその圏構造どうしを「関手」（functor）によって次々に両立させていけるでしょう。あのへんもすこぶる編集的だよね。写像的な双対性が発見できる。
アサト	そうなんです。そういうところが編集工学を圏論でスタディしてみるとわかりやすいんです。圏論は「数学の言語」になっていて、集合論やトポロジーが構成要素になってますから。
イーディ	でも数学のレベルが高いので、みなさんにとってわかりやすくなるかしら。
校長	ま、そこはアサトにがんばってもらおう。圏論が編集的な数学だろうことはまちがいないけれど、では編集思考の特徴を数学的に見ていくのに圏論だけでいいかというと、もっといくつもの見方を複合してもいいんでね。
イーディ	そこで校長！
校長	はい。
イーディ	新年第１弾の千夜千冊として、数学への編集的な入口を示唆してもらえる一冊を推薦してほしいんです。基礎的な本がいいです。
校長	その話ね。基礎的というならそれこそいっぱいあるでしょう。プラトン（７９９夜）もデカルトもライプニッツ（９９４夜）もカントールも、それこそフェリックス・クラインも。高木貞治の『数の概念』（岩波書店・講談社ブルーバックス）や岡潔（９４７夜）の『数学を志す人に』（平凡社）もいいよね。
イーディ	そういう古典名著のほうではなくて、数学を学ぶための認知的で編集的な手掛かりがわかる本です。
アサト	数学的な認知のしくみやその学習心理過程が見える本がいい。
校長	そういう本ねえ。森田真生くんの『数学する身体』（新潮社）とか、「３＋４」を５と答えた子供に〇をつけて話題になった谷口隆くんの『子どもの算数、なんでそうなる？』（岩波科学ライブラリー）とか？　『圏論の地平線』にも登場していた加藤文元の『数学の想像力』（筑摩書房）などもおもしろい。本格入門的なものとしては津田一郎（１０７夜）の『心はすべて数学である』（文芸春秋）や『数学とはどんな学問か？』（講談社ブルーバックス）がいいんだけれど。
イーディ	津田さんのものはちょっと難しかったです。
校長	そう？　となるとこれが一番というものは思い付かないけれど、そうだなあ、だったらノッポ先生かな。
イーディ	ノッポ先生？
校長	うん、デービッド・トールの『数学的思考』（共立出版）。日本の数学教育界ではトール先生で通っている。世界中でトール先生から微積分を教わった者は数知れないみたいね。かなり基礎的な本です。

圏の概念イメージ図。動的な矢印の本質を、射という数学的概念として定式化している。
西郷甲矢人・能美十三『圏論の道案内』（技術評論社）p,21より

アサトによる圏論×編集工学の研究成果の一部。圏論から［守］の「つなぐ／かさねる：用法２」の型を眺める試みである。要素と要素の関係のみならず、関係の関係や発展する関係、意味が現出する関係など、メタ的視点を導入し「つなぐ／かさねる」を数学的に再解釈している。圏論という高度な数学的概念に、守の日常的なお題と本質を同じくする箇所がいくつもある。

イシス編集学校の「伝習座」で、研究成果を発表するアサトこと中村麻人。イシスのiGen世代を代表する中村は、代数学によって「見立て」と「アナロジー」を解釈するなど、数理モデルによって編集工学の可能性を広げる意欲的な試みで、他の指導陣に刺激を与えている。（写真：後藤由加里）

50[守]で「異次元イーディ教室」の師範代を担当するイーディこと新坂彩子。教室名の「イーディ」は、20年来憧れてきたアメリカの女優イーディ・セジウィックのフラジリティに肖りたいという想いからつけられた。（写真：後藤由加里）

イーディ	ノッポ先生ってどういう先生ですか。
校長	トールはマイケル・アティヤ（フィールズ賞受賞）のもとで、トポロジーの研究によってケンブリッジ大学から学位を与えられた数学者です。そういえばアティヤには『数学とは何か』（朝倉書店）といういい本があったよね。アティヤは数年前に８９歳で亡くなったけれど、その歳で微細構造定数をリーマン予想で証明しようとしてたでしょう。凄かったよね。　で、トール先生はサセックス大学をへて、いまはウォーリック大学の名誉教授だね。微積分を教えたりしているうちに、子供たちがどのように分数や関数を理解していくかに関心をもって、数学教育そのものにとりくんで、やがて「プロセプト」理論や「数学三世界」理論などを提唱した。ちょっとユニークな先生です。オペラの指揮をするようなところがあるエレガントな趣味の持ち主みたいね。
イーディ	（スマホをググって）あら、ダンディなおじいさん。
アサト	プロセプト理論と数学三世界？　気になりますね。
校長	うん、「プロセプト」（procept）というのはね、新しい関係を引き出すために柔軟な記号化をはかったり別の構造を任意に措定していくという方法で、プロセスとコンセプトをまぜた造語です。「数学三世界」のほうは、数学には概念的な抽象化と操作的な記号化と公理的な形式化という三世界が一緒くたに動いているのだから、これらを一緒に学習していくほうがいいという、トール先生お得意の見方だね。このことは、もう少し前提的な話をしてからのほうがわかりやすい。
アサト	はあ、その前提的な話というと？
校長	数学はなんらかの理論に新たな経験を付け加えることで発展してきたものではないわけだよね。数学的であるとは、数学の記号表現のしくみを借りることによって、認識や連想の新たな結び付きが変容しうることを確認する知識構造にどんどん分け入るということです。
アサト	数学も編集も知識構造に分け入る。
イーディ	幼児や子供のころはべつとして、ずうっと経験に頼るんではなくて分け入る。
校長	そうだね。知識構造に分け入るには、むろんさまざまな人文学や技芸や科学の領域（ドメイン）ごとに発達してきた方法がありえます。植物を育ててもいいし、哲学に与しても絵を描いてもよく、科学実験を続けてもいいし、世界図をつくってもいい。でもそれらに共通していることがある。　それは一つには、対象の性質を理解するために、知覚を通して何かを入力しているということです。そこにはたいてい、なんらかの情報入力があるんだね。この、さまざまな情報対象をどんな容器（システムあるいはメディア）にｉｎさせるのかというやりかたに、知識構造は左右される。　二つ目には、その情報ｉｎにあたっては、なんらかの操作によるルーチン行為がともなっているということがある。そこでは反復や組み立てがくりかえされます。最近はここをコンピュータの高度な能力を借りて一気にインストールするようにもなったけれど、情報ｉｎのための手続き行為を軽視してはいけない。反復を辞さないような、少しめんどうなくらいがいいと思います。それから三つ目には、この作業にはいつしか言語や記号や線や器具をつかって高度な表現思考に達しようとすることがおこるということです。　このように知識構造に分け入っていくとき、われわれはことごとく編集的になっているんだよね。
イーディ	情報ｉｎのとき？
校長	そうです。ジェローム・ブルーナーが強調したことだけれど、われわれの表現とコミュニケーションのしくみは、もともと３つほどのスキルを試しながら進んでいきます。①動作的であろうとする（動作やジェスチャー）、②画像的に理解しようとする（絵や図表）、③記号的に処理しようとする（言語記号と数学記号）、この３つ。　他に会話する、教えてもらう、読む、なども入るけれど、ここでは３つにしておきます。われわれはこの３つのモードをもって表現思考に向かっていくわけです。この３つ目のどこからかで数学的思考が始まっていく。どこからかということは、足し算や引き算が始まるあたりからということです。
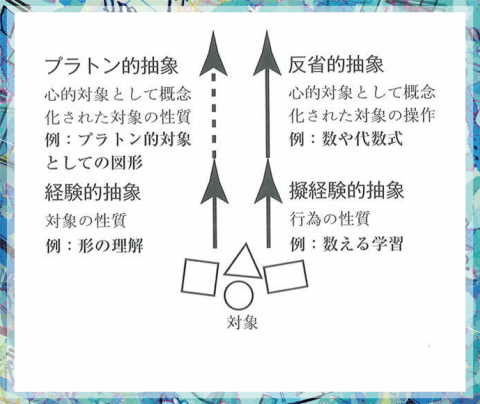
イーディ	子供にもあてはまりますね。
校長	むしろ子供の認知の発達からこそ観察できる。
イーディ	その手の観察は幼児心理学のジャン・ピアジェが先駆的にやりましたよね。ピアジェは子供の認知発達の段階を、前言語的な感覚運動の段階、何かを他者と共有したくて言葉と心をつなげていく具体的操作の段階、道具や考え方をおぼえていく形式的操作の段階というふうに分けました。
アサト	ピアジェはプラトンが心的な対象を抽象すると考えたものを、人間が新しい概念を獲得するプロセスにおきかえて、経験的な抽象、擬経験的な抽象、反省的な抽象というふうになっているとも分けた。これって、どこか数学的思考が発達していくプロセスに似ています。
校長	人間はシンボルとアレゴリーを操る動物なんです。そこから数学も出現してくる。あのね、ズバリ言うと、シンボル（印）とアレゴリー（様子）の操作が足し算とか引き算を成立させたんだね。
イーディ	そこですか。
校長	そこだね。年の瀬のアンガス・フレッチャーの千夜千冊でも書いておいたように、アレゴリーってたんなる寓意のことではなくて、「別様の語り方にする」っていうことだからね。

「数学三世界」のイラストと解説図。数学的思考が発達する３つの方法を示す。①＝黄ゾーンは概念的具象化（人間の知覚と行為→心的イメージへと発展）、②＝緑ゾーンは操作的記号化（物理的行為→数学的手続きに発展）、③＝青ゾーンは公理的形式化（集合論的定義→数学的に証明する）。

プラトン的抽象とピアジェの３つの抽象。
［プラトン的抽象］・・・物理的対象がもつ性質をより抽象化したもので、心の中だけに存在する心的イメージ。［経験的抽象］・・・三角形は三辺をもった図形であることを理解するように、性質を見出して対象を扱う。［疑経験論的抽象］・・・数えたり、分けたり、対象を扱う行為に焦点を当てる。［反省的抽象］・・・ある段階における操作が次の段階で心的思考対象になる。たとえば「数を2倍し、6を足す」計算を、代数式（2x+6）で表すことを保証する。

アサト	シンボルとアレゴリーによる操作が発達してきたのは、どうしてなんですか。
校長	きっと脳の機能が知識圧縮をしようとしているからだろうね。知識圧縮というのはニューロン・ネットワーク上の情報圧縮のことです。
アサト	知識構造に分け入るというのは、知識圧縮や情報圧縮をどうおこすかということですか。そのときシンボルやアレゴリーが動くんですね。
校長	必ずや動いている。メタ編集的にね。『レトリックと人生』（大修館書店）で有名なジョージ・レイコフとマーク・ジョンソンという名コンビがいるよね。二人とも認知科学的な言語哲学者で、メタファーこそが言語の根本的な活動に必須の認知能力のもとになっていると考えた。そのメタファーはレイコフ名付けるところの「概念メタファー」（conceptual metaphor）というもので、周辺的で暗喩的なメタファーじゃありません。たんなる比喩ではない。われわれのアナロジカル・シンキングという根本的な認知活動の要訣を担っているメタファーです。　この概念メタファーを成立させているのがシンボル（記号性）とアレゴリー（寓意性）なんだね。詳しくはレイコフとジョンソンに『肉中の哲学』（哲学書房）というぶるぶるっとする本があるんで、これを読むといい。概念メタファーが入れ子型に出てきます。　で、トール先生はこのことがわれわれに数学的思考をもたらしているとみなしたんです。そういうふうにメタファー思考やアナロジカル・シンキングやシンボルとアレゴリーの活動を通して数学が発達していくことを、認知活動として捉えなおすと、そこに「プロセプト」がおこっているのではないか、そこには「数学三世界」が出入りしているのではないかというのが、さっき述べたトール先生の仮説です。
イーディ	コーフンしてきました。
校長	心おきなくコーフンしなさい（笑）。トール先生の師匠でもあるラファエル・ヌーニェスは『数学の認知科学』（丸善出版）を書いて、もう少しすっきり説明しています。参考になる。
イーディ	気をとりなおして伺いますが、概念メタファーって一般的なメタファーと何がちがうんですか。
校長	ふつうのメタファーの背後にあるのが「概念メタファー」です。ある概念領域を別の概念領域を用いて理解できるとき、そこに概念メタファーが作用したとみなすんですね。移行してみると（あるいは転移させてみると）、それがわかる。
イーディ	たとえば？
校長	わかりやすい日本語の例でいうと、「気分が高揚する」とか「気分が落ち込む」と言うよね。あるいは「成り上がり」とか「落ちぶれる」と言う。ここには「高・下」「楽・哀」「成立・失敗」という対比が動いている。この対比の概念がもたらしている背後からの価値観がないと、こういう言い回しは成立しないよね。　あるいは「荷物を抱える」という表現から「不安を抱える」という表現が出てくるけれど、荷物と不安は別ものだよね。それが言葉をつかっているうちに、つながっていく。あるいは「水を飲む」から「条件を飲む」とか「要求を飲む」という言い方が出たりする。こういうことは上代や古代からしょっちゅうおこっていた。ギルガメッシュや万葉集なんてそんな歌ばかりです。　こういうふうに、われわれは概念すらメタフォリカルに、もっと正確にいえばアレゴリカルに使っているんだよね。これはいいかえれば、概念がそもそもメタファーやアレゴリーを伴って生まれてきたと考えられるということですよ、むしろ概念メタファーから概念がのちに自立していったとも想定できるはずだ。　となるとどうなるかというと、アレゴリーの中に思考様式が芽生えていった、それが哲学や数学になったということなんだね。
イーディ	コーフンします。
校長	心おきなく。

ジョージ・レイコフとマーク・ジョンソン。1979年に出会った2人は西洋哲学や言語学でいうところの「意味」が、生活のなかで実感している意味とまったく違うという認識で意気投合。実際に生活で使用されているメタファーから、言語認識についての考え方に大きな転回をもたらした。

レイコフとジョンソンによる２大メタファー本。『レトリックと人生』（大修館書店）では母国語話者にしかわからない世界＝「言語的中間世界」を形成する最重要なものとしてメタファーをとりあげた。『肉中の哲学』（哲学書房）では、ニューラルなプロセス（認知的無意識）に分け入り、概念システム、カテゴリー、推論のメカニズムを解き、身体から切り離されたマインドの上に成立とされる形而上学のすべて、分析哲学、ポストモダン哲学を、実証的に覆そうとする挑戦的試み。

アサト	ぼくは知識圧縮のことをもう少しはっきりさせたいのですが、どういうことがおこっていると見ればいいんですか。また、その圧縮プロセスのどこで数学的編集が始まっていると見ればいいんですか。
校長	脳が情報や知識を自動的に圧縮して処理していることを、われわれは日々の言葉づかいや計算（アルゴリズム化）や絵をドローイング（視覚による認知）することなどで補助しているんだね。このとき認知心理学的には、少なくとも３つのことが共通しておこっているとみなせます。「カテゴリー化」「カプセル化」「ディクショナリー化」です。　３つとも脳の情報圧縮や知識圧縮がしからしめた手続きで、かつまた言葉やドローイングとともにカップリングされていった手続きです。編集工学ではそこを「単語の目録」化、「イメージの辞書」化、「ルールの群」化と言っているよね。
アサト	はい。
校長	脳とはいってもこれはもちろん「心」でもあるだろうから、この圧縮には心身がかかわっているわけだよね。体と気持ちがね。ということはカテゴリー化、カプセル化、ディクショナリー化はわれわれの「心身の活動」をもろに反映している重大な作業だったということになります。数学的思考や数学的な手続きも、この渦中で派生してくるんです。
イーディ	どの渦中ですか。
校長	初期アルゴリズムの渦中。たとえば７＋３、３＋７、１３－３はそれぞれ計算する手続きがちがうよね。子供はこの計算をたいてい別々に進む。でもこれは「数１０」という知識を分別ゴミにしたようなもので、子供には７＋３、３＋７、１３－３は別々のドラマです。けれども脳の作用としてはいずれも圧縮なんだね。この圧縮がアルゴリズムを発生させていった。
イーディ	すみません、もう少し詳しく。
校長	たくさんのリンゴとミカンがあって、そのうちのリンゴ７つとミカン３つを選ぶ。分配するためにね。次に、たくさんのキャラメルとチョコからキャラメル７つとチョコ３つを選ぶ。こういうことをしていると、このとき７と３という「数」を抽象できてきます。これが当初のカテゴリー化だよね。　次に計算（四則演算）を少しおぼえて「私は７に３を足してます」という行為を自覚していくうちに、「７に３を足すと１０になる」というふうに掴まえるようになる。これがカプセル化だね。カプセルで計算できるようになる。「７に３を足してます」という述語が、新たな「７足す３は１０である」という主語に切り替わるわけです。渦中で移るんです。　このプロセスの変化は数学教育ではＡＰＯＳとよばれていて、Action（行為）、Process（過程）、Object（対象）、Schema（スキーマ）の４つの移動として捉えられているよね。これは学習理論のＳＯＬＯ分類が発展した見方で、ファン・ヒーレやエド・ドゥビンスキーの見方をトール先生が吸収したものです。　ＳＯＬＯというのは“Structure of the Observed Learning Outcome”（観察された学習結果の構造）の略だね、手続き行為が反復されるうちに、手続きをふくんだプロセスが知識圧縮されて一つの事柄になるということです。
アサト	プロセプトされた？
イーディ	なるほど、わかりました。関数の見方が生じるのに似てますね。
校長	そうです、「２倍にして６を加える」が「２（ｘ＋３）」となるようなもんです。

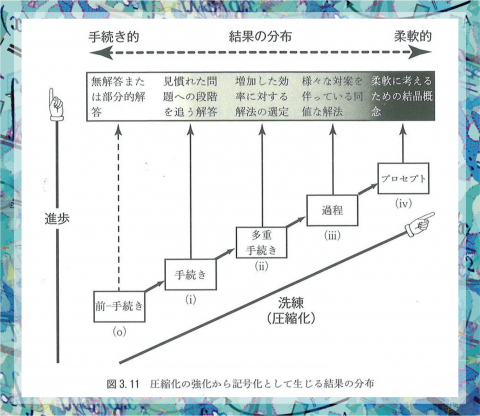
プロセプトにいたるまでの問題解決の諸段階。段階(0)＝［前手続き］において、特定の問題に対して操作的手続きが開発される以前は、無回答もしくは部分的回答かもしれない。手続き的段階(ⅰ)では、特定の手続きを用いてルーティンな問題を解く。多重手続き段階(ⅲ)では、入出力操作として過程を理解しており、その過程を実行できる様々な手続きが対等に捉えられる。プロセプト段階(ⅳ)は柔軟な段階であり、問題中の記号を過程としても概念としても考えられる時期。

アサト	編集工学では「分けると、変わる」「変わると、分かる」と言いますね。トールの数学的思考もそこを展開したんですね。
校長	そこに「の」も加えてね。
アサト	どういうことですか。
校長	編集も数学もどう分けるかが大事です。たとえば「４が３つ分」と「３が４つ分」はちがう。４本の足をもつ猫が３匹と、３本の足をもつ４匹の猫はちがうようにね。けれども「４×３」と「３×４」は同じだとみなすことは、新たな重要な見方です。カプセルやパケットごと動かせば、「３つ分」や「４つ分」にこだわらなくていい。これが算数（アルゴリズム）のすごいところだよね。　でも、数字ではなくて言葉を使うとどうなるかというと、ここが編集の醍醐味になるんだけれど、「薔薇のうちの赤い分」と「赤のうちの薔薇の分」は単純なアルゴリズムにはなりません。「記憶の中のお父さん」と「お父さんの中の記憶」はちがうからね。これは「の」の字の不思議です。言葉は使用する単語（概念）によって「の」の集合力を変えるからね。いや、もともと言葉の多くがそういう集合関係にもとづいて、薔薇＜草花＜植物＜生物という言葉の関係をつくってきたわけだ。　では、この「の」を保存させて計算はできないものか、そこを工夫したのが分数です。分数は「４分の１」（１／４）と「３分の１」（１／３）の「の」を保存したまま計算ができる。そうすると、これが代数に発展します。代数学を意味するアルジェブラ（argebra）の語源のアラビア語は「両方に同じ分が加わっていく」という意味でしょう。
アサト	そこが「の」なんだ。トールは『数学的思考』でそういうことをずっと書いたんですか。
校長	いやいや、本の半ばからは代数学、微積分、連続体、超数学、無限、トポロジーなどをわかりやすくじっくり説明しています。数学三世界的にね。ライプニッツに加担しているところが多かったかな。そして最後に代数学と幾何学を比較して、数学が圧縮と拡張をくりかえしてきた意図をふりかえりつつ、「知性をごまかさないで記述するにはどうするのか」というまとめを書いている。　この本を書くのにあたって影響を受けた本のことも出てきます。ピアジェ、ヴィゴツキーの構成主義理論、バシュラールの認識論、レイコフとヌーニェスの『数学の認知科学』（前出）、チャールズ・パースの記号論、フランシス・クリックの『ＤＮＡに魂はあるか』（講談社）、ジェラルド・エーデルマンの『脳から心へ』（新曜社）などが出てくるよ。読んでみてください。
アサト	読んでみます。
イーディ	トール先生の本が千夜千冊になるんですね。
校長	うん、きっと意外な構成になってね。まあ、アップロードをお楽しみに。今年もよろしく。

4個ずつ3行または3個ずつ4列。ピアジェによれば、数の保存概念を獲得している子どもはあるまとまりが与えられたとき、どこから数えたとしても、いつでもその要素の個数は同じであることを理解し、3×4と4×3を同じものと見なす。数学と編集の分岐点なのか。

TOPページデザイン：富山庄太郎
図版構成：寺平賢司・大泉健太郎・梅澤光由・上杉公志

⊕『数学的思考―人間の心と学び―』⊕
∈　著者：デービッド・トール
∈　監訳：磯田正美・岸本忠之
∈　訳者：添田佳伸・木根主税・渡辺耕三ほか
∈　編集：大越隆道
∈　発行者：南條光章
∈　発行所：共立出版株式会社
∈　印刷所：精興社
∈　製本：ブロケード
∈　発行：2013年

⊕ 目次情報 ⊕
∈∈　第I部　前奏
∈　第1章　本書について
∈∈　1．数学について思考する子ども
∈∈　2．数学的思考の長期発達
∈∈　3．理論枠組み
∈∈　4．概念と過程の両方を表す記号
∈∈　5．知識圧縮
∈∈　6．数学三世界
∈∈　7．我々が持つ能力
∈∈　8．経験に基づく知識
∈∈　9．「生まれつき備わっていること」と「以前にみたこと」
∈∈　10．知識構造の結びつき
∈∈　11．数学学習の情意的側面
∈∈　12．結晶概念
∈∈　13．簡単な概観

∈∈　第II部　学校数学の背後にある論理とその因果性
∈　第2章　数学的思考の基盤
∈∈　1．言語
∈∈　2．図形の初期経験
∈∈　3．意識的思考の3つのレベル
∈∈　4．幼児期の数概念
∈∈　5．計算の初期段階
∈∈　6．過程と概念としての記号
∈∈　7．結晶概念としてのプロセプト
∈∈　8．算術の成果における相違
∈∈　9．振り返り
∈　第3章　数学的考えの圧縮化・結びつけ・融合化
∈∈　1．思考可能概念への圧縮化
∈∈　2．カテゴリー化
∈∈　3．カプセル化
∈∈　4．定義づけ
∈∈　5．思考可能概念と知識構造
∈∈　6．要約
∈　第4章　生得的構造・経験的構造・長期学習
∈∈　1．生得的構造の概念
∈∈　2．経験的構造
∈∈　3．支持的概念と問題提起的概念
∈∈　4．要約
∈　第5章　数学と情意
∈∈　1．用具的理解と関係的理解
∈∈　2．スケンプの目標と反目標の理論
∈∈　3．数学不安
∈∈　4．一般化と拡張による融合
∈∈　5．支持的概念と問題提起的概念
∈∈　6．目標と成功
∈∈　7．結び
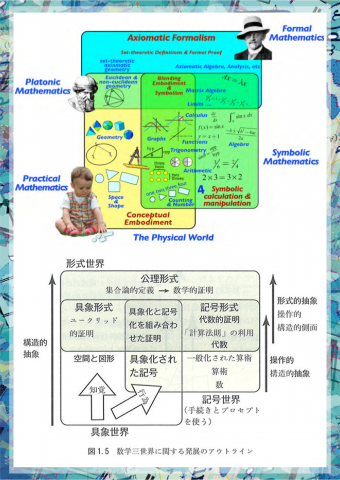
∈　第6章　数学三世界
∈∈　1．数学三世界
∈∈　2．具象
∈∈　3．概念的具象世界
∈∈　4．具象化から操作的記号化への移行
∈∈　5．公理的形式世界
∈∈　6．これまでの話
∈　第7章　具象世界と記号世界を通る旅
∈∈　1．知識構造の圧縮
∈∈　2．具象世界における高まっていく複雑さ
∈∈　3．帰結
∈∈　4．具象世界、記号世界、そして形式世界の長期的な発展
∈　第8章　問題解決と証明
∈∈　1．問題解決
∈∈　2．授業研究
∈∈　3．証明についての思考
∈∈　4．形式的証明

∈∈　第III部　間奏
∈　第9章　数学の歴史的進化
∈∈　1．記数法の発展と初等算術
∈∈　2．幾何学と証明の発展
∈∈　3．代数学の発展
∈∈　4．代数学と幾何学を繋ぐ
∈∈　5．微積分
∈∈　6．複素数の意味づけ
∈∈　7．現代の形式主義的数学の誕生
∈∈　8．コンピュータの役割
∈∈　9．要約

∈∈　第IV部　大学数学とその先
∈　第10章　形式的知識への移行
∈∈　1．具象世界および記号世界から形式世界への主要な革新
∈∈　2．集合と関係
∈∈　3．実数と極限
∈∈　4．自然なアプローチと形式的アプローチ
∈∈　5．理論枠組みの比較
∈∈　6．さらなる大きな図
∈∈　7．考察
∈　第11章　微積分に見る考えの融合
∈∈　1．微積分概念の起源
∈∈　2．微積分指導の問題点
∈∈　3．微積分への局所直線アプローチ
∈∈　4．ライプニッツの再訪
∈∈　5．媒介変数関数
∈∈　6．合成関数と連鎖律
∈∈　7．逆関数
∈∈　8．極限概念の導入
∈∈　9．動的に具象化された連続から形式的な定義へ
∈∈　10．連続なグラフ下での面積
∈∈　11．微分方程式
∈∈　12．偏微分
∈∈　13．具象化と記号化の関係
∈∈　14．省察
∈　第12章　数学者の思考法と構造定理群
∈∈　1．初学者と専門家の比較
∈∈　2．証明過程と真であることの保証
∈∈　3．構造定理群および具象世界と記号世界の新形式
∈∈　4．選択と帰結
∈∈　5．新たな組織化原理
∈　第13章　無限小を熟考する
∈∈　1．無限大と無限小に対する対照的信念
∈∈　2．無限小を含む順序体
∈∈　3．無限小を用いる微積分学
∈∈　4．超実数を作る
∈∈　5．教育上の帰結と局所直線性
∈∈　6．微分可能な関数を拡大する
∈　第14章　数学研究におけるフロンティアの拡大
∈∈　1．問題の解決と定理の証明
∈∈　2．形式世界における数学的理論の多様性
∈∈　3．幾何学と代数学の発展の対比
∈　第15章　回想
∈∈　1．理論全体を見る
∈∈　2．数学における思考可能概念の発達
∈∈　3．数学三世界を通じた人々の旅
∈∈　4．通用する内容と通用しない内容に関連する情意
∈∈　5．拡張的融合
∈∈　6．理論枠組みの発展：通用する内容と通用しない内容
∈∈　7．指導への示唆
∈∈　8．理性的思考

∈∈　結語
∈∈　付録　本書の着想の出所
∈∈　引用文献
∈∈　解説
∈∈　監訳者あとがき
∈∈　事項索引
∈∈　人名索引

⊕ 著者略歴 ⊕
デービッド・トール（David Tall）
1941年生まれ。オックスフォード大学のマイケル・アティヤ教授のもとで博士号を取得（哲学）。ウォーリック大学名誉教授。とりわけ、同大学の大学数学教育研究センターを拠点としたエディ・グレイとの共同研究は数学教育界でよく知られている。著書は『数学的思考』（2013）他多数。音楽にも造詣が深く、ヴィオラ演奏や指揮の他、音楽団体の立ち上げなどにも携わる。

⊕ 監訳者略歴 ⊕
礒田正美（いそだ・まさみ）
筑波大学大学院修士課程教育学研究科修了。現在、筑波大学教育開発国際協力研究センター長/人間系教授、博士(教育学):早稲田大学、国際数学歴史教育学会顧問委員、コンケン大学名誉博士、イグナチウスロヨラ大学名誉教授。専門は数学教育学。主著に『算数・数学教育における数学的活動による学習過程の構成』（共立出版、2015）、『曲線の事典：性質・歴史・作図法』（共編、共立出版、2009）がある。
岸本忠之（きしもと・ただゆき）
1968年生まれ。筑波大学大学院博士課程教育学研究科単位取得退学。現在、富山大学人間発達科学部教授、修士(教育学)。専門は数学教育学。主著に『数学科・デジタルテクノロジーで広がる学習環境の創造―インターネットによる数学コンテンツを活用した指導実践―』（編纂、明治図書、2007）、『身近な題材で始める数学教材ハンドブック：「資料の整理と読み」の力を伸ばす授業プラン』（編纂、明治図書、2015）がある。