非線形科学

　リズムというと、ほとんどは音楽の領域の話題だと考えられがちだが、この３０年でリズムおよびリズム振動が非線形科学の最も重要な現象であることが立証されてきた。とくにリズム振動が相互におこす同期現象は自然界から社会生活にいたるまで、数多く発見されてきた。
　リズムは状態空間のなかのアトラクター（状態点の集まり）である。ということは、リズムはカオスやリミットサイクルでおなじみの非線形科学の主人公のひとつだったのだ。また、散逸構造の特徴を「しかるべきところに落ち着く」というふうに見れば、リズムは散逸構造を代表する現象だった。
　本書は非線形科学についての、できるかぎり基本的な見方を提供しようとしている好著のひとつだろう。科学解説書でありながら、たいそう想像力に富んでいる。科学の不得意な諸君にも薦めたい。著者の蔵本由紀は、京大の基礎物理学研究所のリーダーの一人で、１９７５年に自然界の同期現象についての数学モデル「蔵本モデル」で世界的に知られた。ヘルマン・ハーケンの研究や清水博の研究とも併走していた。やや遅すぎる評価であったが、２００５年には非線形科学の先駆的研究で朝日賞を受賞した。
　その蔵本さんが、めずらしく一般向けの本を書いた。こういう本が書けるとは思っていなかったらしいが、これが新書のよさというものだろう。あとで紹介するが、本書には注目すべき考え方も示唆されている。非線形科学の本質はメタファー（隠喩）に似ているというものだ。

　多くの科学者の仕事は、「不変なもの」を通して「変わっていくこと」をどのような説得力をもって語るかということにある。そのためにはまず自然界の不変な構造をさぐりあて、それを記述するための削がれた表現手段をつかう。それが数理言語（数学や数式）というもので、それを使って「不変なもの」を列挙する。
　こうして恒常的な法則がいくつか導き出せるようになると、そのうえで、「もの」と「もの」とのあいだの「変わっていくこと」を方程式であらわしていく。ガリレオの落体の法則がそうやってつくられた。これが古典力学と線形科学の常套手段というものだ。
　しかし、すべての現象が「不変なもの」を基礎にして「変わっていくこと」になっていくとはかぎらない。「不変なもの」とは関係なく、一見、自律的に「変わっていくこと」がおこっていると見たほうがいい現象もある。この現象を説明するために非線形科学が登場してくる。

　線形（linear）や非線形（non-linear）というのは数学用語である。線形は変化の度合いがほぼ一定で、グラフにすると直線になる。植物の枝や葉脈、道路や鉄道などの路線が線形だ。こういう線の特色はいくら混みあっていても数学的には一次式（またはその近似式）であらわせる。線をつくっている原因と結果の関係が比例であらわせるからだ。工夫さえすれば重ね合わせができる。
　非線形とは線形であらわせないすべてのことをいう。グラフにしても直線的ではなく、重ね合わせはできない。重ね合わせをしようとしても、その一回の試みや次の一回の試みが、それまでの結果を上回ってしまう。少しの変化が大きな変化を生んでいくのが非線形な現象なのだ。
　蔵本さんは、非線形の特色を「同期」という現象を通してつぶさに観察してきた。そういうことを深く研究するきっかけになったのは、ルネ・トムの『構造安定性と形態形成』（１９７２）が提示したカタストロフィ理論を知ってからだったという。カタストロフィ理論は非線形な「散逸力学系の分岐現象」に属していた。
　そのあと蔵本さんは九州大学物理学教室の助手時代に清水博さんに出会い、アーサー・ウィンフリーの振動子モデルの論文を見せられて、非線形科学にのめりこんでいった。ウィンフリーは生物時計を研究していた。ベロウソフ・ジャボチンスキー反応の不思議をみごとに整理した数学モデルだった。清水さんは当時の日本の非線形科学の立役者だった。

「世界でいちばん受けたい授業」清水博さんの特別講義。
連塾２第四祭「浮世の赤坂草紙」より
（撮影：川本聖哉）

　アイロンやエアコンのような温度制御装置は、単純な非線形システムの例である。温度の上昇と下降の「あいだ」を切り替える自動制御機構がそこを担っている。
　生物現象にも非線形はあらわれる。栄養物が入った容器でバクテリアを増殖させると、増殖の速さはバクテリアの総量に比例する。ここまでは線形的なのだが、栄養物が少なくなってくると、バクテリアの動きは鈍る。比例関係は成り立たなくなってくる。容器ともども非線形システムが動きだしたのだ。
　わかりやすくいえば、非線形システムとは「システムの状態に応じてその変化を自己調節しているシステム」のことをいう。アイロンやエアコンでは基準温度からのズレがシステムの一方向性を変化させ、容器のなかのバクテリアでは、増殖の進行そのものが増殖をおしとどめる原因をつくる。
　このような自動調節機構でおこっているのは「負のフィードバック」である。現象の行きすぎを咎める方向が自動的におこるので、この名前がある。これに対して「正のフィードバック」では、富める者がますます富むというように、過剰に向かってシステムが進む。
　正のフィードバックと負のフィードバックは、多くの生命組織でまことに自在にくみあわさって動いている（生命で一番重要なのはこのことだ）。生命組織は非線形システムの宝庫なのである。たとえば脳の神経ネットワークを構成する無数のニューロンは、そのひとつひとつが非線形ユニットになっている。
　もちろん物理現象にもさまざまな非線形システムが動いている。しかし、その現象の全体が最初から非線形であるということは、ほとんどない。システムが非線形になるのは、ダイナミック・システムの動向の途中からであって、そこに「相転移」（phase transition）や「創発」（emergence）がおこってからなのである。「不変なもの」と「変わっていくこと」とのあいだにおこっているのは、この「相」を劇的に変える「相転移」や「創発」だった。

　地球は宇宙のなかでは平均的な星ではない。かなり変な星である。エネルギーとエントロピーの入口と出口をもっていて、生成されるぶんだけのエントロピーを排出するようになっている。そうすることで地球全体としては統計的な定常性を保つようになってきた（地球温暖化などはこの定常性に狂いが出てきた兆候だ）。これが狂うとブライアン・オールディスの「地球の長い午後」になり、Ｊ・Ｇ・バラードの「時の声」がやってくる。
　このような地球の状態を熱力学の用語で「非平衡開放系」という。宇宙中心がつくる平衡力からやや自由で、熱の出し入れができているという意味だ。生命の歴史はこの熱力学的に非平衡で開放的な性質を活用して誕生した。とくに循環エネルギーと化学結合のエネルギーを活用した。
　太陽によって温められた地表と上空とのあいだには、つねに大きな温度差が生じている。暖房中の室内の空気が循環するように、この温度差が駆動力となって大気が循環し、それによって気象が生じる。この駆動力は上昇した水を冷却して、それを雨に変えて地表に降り注がせもする。その水の循環エネルギーが地球の外部にエントロピーを放出する大きなエンジンにもなる。地球の内部は内部で、マントル対流などが循環エネルギーのエンジンとなって、われわれには脅威だが、ときおり火山爆発や地震や津波をおこしてエントロピーを調整しているわけだ。
　こういう内外にわたる地球のシステムを、熱力学では「散逸構造」（dissipative structure）という。御存じ、イリヤ・プリゴジンの命名だ。この散逸構造のふるまいを扱うには非線形科学が必要になる。というよりも、われわれが地球に生まれた以上、生命が感知する多くの現象は非線形科学の対象にならざるをえないと言ったほうがいい。
　散逸構造は、地球のような大きなシステムだけではなく、小さな場面にもいろいろあらわれる。そこでは化学結合エネルギーが活躍する。とくに流体運動の多くの場面、たとえばウロコ雲や鍋の中のスープや熱い味噌汁にもあらわれる。流体運動でこのようなパターンができてくるのは、そのシステムが散逸構造になってからなのである。それを運動方程式にすれば、ナヴィエ・ストークス方程式というものになる。
　こうした循環エネルギーや化学結合エネルギーにおいて、共通して特徴的なことがおこっていた。そのシステムに「リズムが生じる」ということだ。蔵本さんの専門は、このリズムが生じさせるリズム振動子の同期についての研究だった。

「カルマン渦列」と呼ばれる流体運動のパターンの例。
済州島のハンナ山に季節風が吹きつけ、
その南部に相似性をもった雲がいくつも生じている。

　世の中にはいろいろのリズムが動いている。四季の移り変わり、潮の干満、昼夜のサイクル、海岸に打ち寄せる波、呼吸や心拍、コオロギの鳴き声、時計、ピアノの演奏、コンピュータのなかの高周波……。いずれもリズムをつくる。
　このようなリズム現象には、そのメカニズムがすぐわかるものも、わからないものもある。日本庭園で甲高い音をたてる「ししおどし」や多くの歯車時計は、ごく単純なリズムを打っている。それらとはべつに、リズムの発生機構がすぐには見当がつかないものも少なくない。コオロギの鳴き声やホタルの明滅のリズムは、どのようにしてそうなるのかが、なかなかわからない。それでもリズムが出てからあとの現象の分析にとりくむことによって、そのリズムの性質をさかのぼって判定することができる。これに注目するのが非線形科学によるリズム論なのである。
　リズムには妙な性質がある。単一のリズムを見ているだけではわからない。２つ以上のリズムを観察すると、その妙な性質がときに見えてくる。ＡのリズムとＢのリズムが出会っていくと、そこにリズム間の「同期」（シンクロナイゼーション）や「引きこみ」（エントレインメント）がおこるのだ。
　このことに最初に気がついたのは１７世紀の天才クリスチャン・ホイヘンスで、二つの振り子時計を別々に進行させておくと、いつしか振り子が同期した。数時間もすれば狂いが出てきそうなのに、それがおこらない。それどころか、わざと揺れのタイミングをずらしても、すぐに２つの振り子は同期した。
　ホイヘンスの振り子時計は、外部からエネルギーの供給をうけてエントロピーを生成しつつ、それをエネルギーとともに外部に排出している散逸力学系の振動である。これをリミットサイクルの振動という。周囲の状態点を引きつけてくる軌道（閉軌道）なのでリミットサイクルといい、その周期的で安定的な運動をリミットサイクル振動という。総称して「リズム振動」（その点をリズム振動子）ともいう。ここに「同期」や「引き込み」がおこる。このリミットサイクルがどんどん増幅して不安定な振幅になっていくとカオスが生じる。

　リミットサイクルは生物やわれわれの知覚にも届いている。生︲情報系でもあらわれる。有名なのはサーカディアン・リズム（概日リズム）で、いわゆる体内時計が感じている一日周期のリズムをいう。およそ生物の多くはなんらかの体内時計の装置によって、このサーカディアン・リズムを感知する。ということは、生物はみな地球の自転を感知しているということになる。これは、生命体そのものがそもそもリズム振動子の集合だということを意味する。
　ホイヘンスの振り子はそのリズムが互いに歩みよっていたので、こちらは「相互同期」という。サーカディアン・リズムのほうは地球全体にあってきわめて絶対的なので、このリズムに同期することは「強制同期」である。しかしこれらのリズムの同期は、ある状態では意外な現象をおこす。それが集団同期現象になる。
　ヒュー・スミスが発表したホタルの集団明滅にひそんでいた同期現象は、そうした集団同期現象のひとつだった。ＭＩＴのスティーヴン・ストロガッツが分析してみせた橋梁が崩落する現象も集団同期現象だった。オペラハウスやコンサート会場での拍手の同期にも似た現象があらわれる。ストロガッツは蔵本さんの数十年来の知己で、名著『非線形ダイナミクスとカオス』（丸善出版）や『ＳＹＮＣ』（早川書房）が唸らせた。ＳＹＮＣはシンクロニシティの数理を扱っていた。
　こうした同期現象には結論的にいえば相転移がおこっていたのである。相転移には物理量が不連続に変化する一次相転移と、転移点ははっきりしているけれど物理量の変化のない二次相転移があるのだが、この二次相転移にもっと重要な現象が派生する。それを非線形科学では「ゆらぎ」（fluctuation）と言っている。

　そよ風の性質、モーツァルトのメロディ、読みかけの本のページの文字の濃度、心臓の鼓動、列車の音……。「ゆらぎ」はさまざまな場面に観察できる。
　ふつうの科学では、「ゆらぎ」は平均値からはみだした箇所の現象をいう。平均積雪量や標準血糖値より多かったり少なかったりするのが「ゆらぎ」であって、そこには平均値というものがあって、そこにゆれ幅が出るのが「ゆらぎ」だとおもわれている。しかし、平均値というような基準になる値が確定できない「ゆらぎ」だけの現象もある。それが二次相転移によくおこる。
　鉄やニッケルなどの金属は常温で磁気をもっている。それを非常に高温にすると、その性質が失われる。鉄のばあいは７７０度で磁気を失う。７７０度が磁気に関する相転移点をあらわしている（磁気相転移という）。金属の多くは構成分子がミクロな磁石になって磁性をつくっている。単位面積あたりの磁気モーメントであらわす。これは方向をもった量、すなわちベクトルである。ミクロなベクトルは近隣どうしで向きをそろえるような力を及ぼしあっている。ところが高温では、激しい熱運動がおこるために、ミクロなベクトルがばらばらに方向を打ち消しあう。これを今度は臨界温度（キュリー温度）以下に冷やしてやると、方向をそろえる効果が熱運動に打ち勝って、そこに磁気があらわれる。
　何がおこったのかというと、ミクロなベクトルの「ゆらぎ」が互いの自律性をこえて相関性をもった。端的にいうなら「ゆらぎ」が新たな秩序をつくりだしたのだ。
　ミクロな要素が、そのシステムのなかで新たな相関関係をもつときに「ゆらぎ」が創発し、そこから秩序が生まれているということは、きわめて興味深い現象だ。ここには従来の科学ではなかなか予想できなかった世界観がひそんでいた。
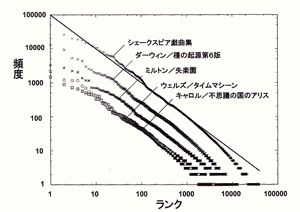
　ひそんでいたものから、何が見えてきたのか。平均値や中心極限定理では説明できない「自己相似性」のようなものがシステムに生じてきたのである。非線形科学では、この自己相似性を「ゆらぎのパワースペクトル」（強度分布）としてあらわし、それがベキ法則に従うことをつきとめた。また、ここからは自己組織的臨界状態の研究がいくつも派生した。さらにまた、この研究のかたわらで、有名な「 ゆらぎ」や「フラクタル」が発見されたのである。

ベキ法則に従って「ゆらぎ」が秩序を作る例。
１つの書物に現れる単語の出現頻度は、
頻出度の順位にほぼ逆比例する。
このような法則を「ジップの法則」と呼ぶ。

　従来の科学は「不変なもの」を通して「変わっていくこと」を発見しようとしてきたと、先に述べておいた。そのため、科学の趨勢は世界をマクロな法則とミクロな法則とで成立していると考えて、このうちのマクロ現象を根底で成立させているのが、エネルギー保存の法則とエントロピー増大の法則であるというふうにみなしてきた。
　エネルギーには力学エネルギー・電気エネルギー・化学エネルギーなどがあり、たとえば水力発電では水の力学エネルギーが電気エネルギーに変わり、ブランコでは運動エネルギーが空気中の分子の熱エネルギーとせめぎあっている。そのようにエネルギーはさまざまなかたちに変換され競争しあうけれど、そのエネルギーの総量が食い違うことはないというように、辻褄をうまく合わせるようにしてきた。
　しかしながら、このような見方は、世界を「主語」によって包摂するという方法なのである。たしかに従来の科学は「何」（主語）が、「どのように」（述語）あるかということを記述するものであるけれど、それでは理解できないこともある。説明がつかないこともある。では、どうするか。この見方をひっくりかえしたらどうなのか。すなわち、「どのように」という世界に、さまざまな現象の「何」や「何々」がおいてあるというふうに見てみるのである。かつてデヴィッド・ボームが量子力学の言語化のため、動詞によるレオモード（流態）を考案しようとしたことが、思いあわされる。
　これは「主語から述語を見る科学」が、「述語から主語を見る科学」に変わるということだ。いろいろ計算モデルをつくってみると、このひっくりかえしがおこる現象として、さまざまな非線形科学の対象があらわれた。
　本書がおもしろいのは、ここなのだ。蔵本さんは、すでに『新しい自然学』（岩波書店→ちくま学芸文庫）において「述語的統一による科学」の提唱をしている。あまり詳しくない説明ではあったものの、これは、ぼくがユクスキュルやホワイトヘッドやフレーゲやポランニーやボームに触発されて、約４０年にわたって憧れてきた科学像でもあった。ただ、いっこうに成果が乏しかった。それがやっと非線形科学の一部が述語的になってきたのである。今夜、本書を紹介したのは、その成果の香りのゆらめきを嗅いでほしかったからだ。

　本書の最後では、述語的自然学の可能性がふれられている。「不変なもの」を通して「変わっていくこと」を求めるのではなく、「変わっていくこと」のほうを述語的世界として広くとって、そこから逆に「不変なもの」を新たに見いだそうという科学の可能性を述べたくだりだ。
　こうして蔵本さんは、最後の最後になって次のような示唆深いことをのべて、本書をおえる。比喩や暗喩のはたらきこそ、新たな科学像を導くための有効な方法ではないかという示唆だ。ロジカル・シンキングからアナロジカル・シンキングへ。蔵本さんはその可能性をひらいたのだ。これは、まさに“編集的科学”の予兆を感じさせるものだった。こんなふうに綴っている。
　「非線形科学で見いだされた現象横断的な不変構造は、たんに述語的というよりも比喩、とりわけ隠喩に近いはたらきをもっているように思います。隠喩とは、たとえば“玉虫色”とか“氷山の一角”という表現にみられるように、元来なんの関係もない異質な二物が突如結びつくことで新鮮な驚きを誘発する表現技法です。それに似た意外性が、非線形科学における現象横断的な不変構造にはあるのです」。