自己組織化と進化の論理

　生命の最も初期の痕跡は３４億５０００万年前の化石に記録されている。今日の生物でその化石に近いものは深海にいたシアノバクテリア（藍藻）だ。そこには最も原初的な生体膜（細胞膜）が認められる。
　生命は物質代謝や生殖の能力があり、分化や進化ができる能力がある。その能力は生体膜の内側に生じた細胞によっている。その細胞が異常な化学進化をするうちに、われわれはいつしかそれを「生物」とよぶようになった。
　いったん細胞ができてからは、気の遠くなるような時間がわれわれの祖先におよぶまで流れた。単細胞生物ができ、ついで初期の菌類のさきがけにあたる筒状の細胞たちができ、これらが集まって協調しながら数メートルの広がりと高さをもった小丘のような複雑な構造を用意した。これはその後のあらゆる生態系の基礎となったモデルだ。いまでもこれに似た小丘がオーストラリアのグレートバリアリーフのストロマトライトとして眺めることができる。ここまででざっと３０億年。
　こうして８億年前に多細胞生物が登場してきた。おそらく筒状の原始菌類が自分の内部に柔らかい膜をつくりはじめたときだったろう。さらに５億５０００万年前のカンブリア紀になって、一斉に多様性の出現がおこった。「カンブリアの大爆発」だ。今日の生物学でいう「門」にあたる多くの生物がここで生み出された。
　
　地球上のあらゆる生物は「種」と「属・科・目・綱・門・界」というリンネの分類案によって、いまだに階層的樹状的に区別されている。
　この順は特定なものから普遍的なものへという序列だとみられているが、つまりしだいに「目・科・属……」というふうに進化が多様化していったとみられているが、必ずしもそうとはいえない。そのうちの「門」にあたる多くの生物がカンブリア紀で出現したことは、逆向きの展開や一足飛びの発生をおこす大変動がありうることを示唆するからだ。スティーブン・ジェイ・グールドが死ぬちょっと前に『ワンダフル・ライフ』（早川書房）で書いたのは、この逆向き一足飛びの事態についての真摯な驚きと感動だった。
　グールドはこうした展開の可能性がありうることからみて、進化は必ずしも連続的に進行したのではなくて「断続平衡」をもちながら発展したと推理した。進化のシナリオはナッシュ均衡の連続ではないという見解だ。ナッシュ均衡というのはゲーム理論の用語で、それぞれが最適な戦略を選んで互いに均衡しあうことをいう。グールドは、進化はそういう均衡点の連続でできあがったものではなく、ときに前後の見境いがつかなくなるような断続があったというのである。
　一方、細胞が多細胞生物に向かうという「種」や「門」の秩序づくりのドラマとはべつに、生命にはＤＮＡやＲＮＡからはじまる情報それ自身のドラマがあった。遺伝子による情報の歴史というものだ。
　遺伝子が何をしたかといえば、生命プログラムという情報様式の自己複製システムをつくりだした。生命はこの自己複製がなければここまで進化しなかった。そこで動物行動学の貴公子リチャード・ドーキンスは遺伝子こそが進化の中心的な主人公であって、したがって遺伝子は自分の利益を維持するために生物の多様性を利用しているのだという「利己的遺伝子」の仮説を唱えた。
　利己的遺伝子説では、生物たちはナッシュ均衡を求めあうように進化したと考えられている。遺伝子が生物たちをそうさせるように仕向けたというのだ。この仮説からすると、「種」や「門」は遺伝子のヴィークル（乗り物）にすぎない。しかしはたしてそうなっているかどうかは、まだまだ結論は出しがたく、グールド派の仮説とドーキンス派の仮説はいまなお対立したままなのである。
　
　さて、そこで本書の登場になる。本書の著者のスチュアート・カウフマンはグールド仮説にもドーキンス仮説にも不満をもった。もっと新しいパラダイムから進化の謎を解きたいと考えた。そのパラダイムは「複雑系の科学」にあった。カウフマンはサンタフェ研究所に所属するようになってから新たな仮説にとりくんでいく。
　われわれは多様な要素が複雑にからみあった世界の内側にいる。そこでは、あらゆる種類の分子が集まって物質代謝というダンスを踊り、多様な細胞をつくってきた。その細胞は他の細胞と互いに作用しあって、多彩な組織を形成する。カウフマンはこの細胞と組織が生む秩序の生まれかたに注目した。「種」や「門」でも、遺伝子でもなく、その中間にある細胞と組織の秩序がどのようにつくられているのかという見方だ。ここまでは清水博や木下清一郎とほぼ同じ視点といっていい。
　それなら、この細胞の生成と形成をめぐる世界には何かの基本構造とでもいうものがあるのだろうか。もしあるのだとしても、おそらくどんな既存の理論でもうまく説明がつかないだろう。これまではもっぱらダーウィンが教えたこと、すなわち、生物の秩序と多様性はランダムな突然変異のなかから自然淘汰によって、稀有で強力な遺伝子や個体や種が選び出されてきたことによって生じたという説明でしか語られてこなかったのだ。その特色の一面を強調したものがグールド仮説やドーキンス仮説なのである。
　カウフマンは３０年にわたる思索と研究と協力者の示唆にもとづいて、このような見方に不満をもった。そうなるにあたって、カウフマンがオックスフォード大学では哲学と心理学を、カリフォルニア大学では医学を、シカゴ大学では理論生物学を、ペンシルヴァニア大学では生化学と生物物理学を、それぞれマスターし、教授してきたこと、そして最後にサンタフェ研究所に移って「複雑系の科学」の最前線に立たされたことが、うってつけの戦歴となったようだ。
　カウフマンは展望した。自然淘汰はむろん重要なことではあるが、それをもって細胞・組織・生態系におよぶ生物圏の構造を説明することはほとんど不可能だろう。そこにはきっと「自己組織化」というもうひとつの基本構造原理がはたらいているだろう。そう考えたカウフマンは自然淘汰と自己組織化の両方が作用する理論をつくりあげることを決意する。
　
　ぼくがこの分厚い一冊を読んだころ、本書は複雑系に関するサンタフェ研究所関連の成果がもたらした最も痛快な一書だった。当時の帯には“ドーキンスを超える知的衝撃”というふうに銘打たれていたが、これはカウフマンに悪い。ドーキンスのものより扱っている中身がはるかに幅広く、しかもスリルにも富んでいた。比べようがない。
　その後、複雑系をめぐってはかなり大胆な仮説や精緻な論理が提案された。そのなかには金子邦彦や津田一郎の試みも入っていて、ぼくとしてはカウフマンの仮説にばかり加担するわけにはいかなくなったのだが、それでも自己組織化理論のとりあえずの最前線を示す成果として、周囲には本書を読むことを勧めていたものだった。
　カウフマンも本書の五年ほどあとに『カウフマン、生命と宇宙を語る』（日本経済新聞社）で、非エルゴード宇宙における「共構築」（共進化）仮説をまとめ、複雑で多様な宇宙が非エルゴード的に隣接可能領域に侵入しながら共進化をとげつつ自己構築するというフィジカル・ヴィジョンを提出した。そこにさらにペンローズのツイスター理論やスーパーストリング（超ひも）理論やＭ理論（宇宙理論）との共存がありうることも示唆していた。原題はずばり“Investigations”だ。
　そこまで考えるかと感心したり、その過剰気味の仮説に心配したりしたが、カウフマンがあいかわらず理論構築に急速な情熱を注ぎつづけていることはよく伝わってきた。しかし今夜は本書が提示した枠組みだけを案内することにしたい。そのほうが帯が訴える“ドーキンスを超える知的衝撃”がどこにあるかということが、わかりやすい。
　
　１９世紀における２つの際立つ理論の成立、すなわち進化論と熱力学の成立は、われわれが宇宙における「孤立した偶然の存在の一族」に属するのだろうという観念を広く定着させた。とくにカルノー、ギブス、ボルツマンが考察して確立した熱力学第二法則は、大環境の中におけるわれわれの宿命を決定づけた。
　熱力学第二法則は、環境とのあいだに物質やエネルギーのやりとりがない閉じた系ではエントロピーが増大し、その系が平衡状態に達したときにはエントロピーが最大になることを示している。ボルツマンは、気体の分子で満たされた箱を想定して、こうした平衡系においてエントロピーが最大に向かうのは、おそらくシステムが可能なすべての状態をランダムに巡回する統計的傾向をもつからだと推理した。いわゆるエルゴード仮説である。
　水の中に青いインクの滴を落とせば、やがて水を薄い青にする。インクがふたたび集まって青い滴になることはない。同様に箱の中の気体の分子もどこかに集まることはないはずだ。このとき分子は圧倒的な確率で一様に分布しているとみなされる。こうした系では秩序はやがて消えていく。熱力学の言葉でいえば、系がエルゴード的に微視的な各所を動きまわることによって、秩序をおこせるようなすべての可能性が消えたということになる。
　系に秩序が生まれるには、なんらかのかたちで外部から仕事が加わる必要がある。別の色のインクを落とすとか、遠心分離機にかけるとか。ふつうなら、そう考えるところだ。しかし、めざましい例外が２つあったのだ。ある系に秩序が生まれるには、ひとつには、低いエネルギーをもつ平衡状態があってもよかった。わかりやすくいうなら、たとえば「起き上がり小法師」や「丸い鉢の中にあるボール」のような例だ。

　鉢の中にボールを投げ入れてみると、ボールは最初のうちは運動エネルギーでぐるぐる動いているが、やがてはその位置エネルギーが最小になるところで停止する。物理学的にいえば、重力のために生じた運動エネルギーが摩擦によって散逸して平衡状態に達したときに、ボールはぴたりと止まる。ボールが鉢の底という平衡状態に達すると、その秩序を維持するのにそれ以上のエネルギーを必要としなくなる。
　こういう例外は生物現象にもいくらでも見られる。たとえばウイルスは核を形成する繊維状のＤＮＡあるいはＲＮＡからなる複雑な分子システムであるけれど、核のまわりには繊維状の尾や頭部にあたるもの、そのほかさまざまな特徴をつくるタンパク質が集まっている。水に富んだ適当な環境のもとでは、そうしたＤＮＡやＲＮＡの分子と構成要素のタンパク質がちょうど鉢の中のボールのように最小のエネルギー状態をさがして自発的に集合し、ウイルス粒子をつくっていく。いったんウイルス粒子がつくられれば、それを維持するのにそれ以上のエネルギーは必要ではなくなる。これが平衡系における秩序の生まれ方のひとつである。
　もうひとつの例外は、非平衡系における秩序の生まれ方だ。ここでは秩序化された構造を維持するために、質量あるいはエネルギー、またはその両方の供給源が必要になる。たとえば浴槽の中で排水口に向かってつくられる渦巻だ。
　浴槽の水は排水口をあけたとたんに水が連続的に供給されて、この渦巻が一定の時間は壊れない。これが非平衡系に生まれる秩序の例である。木星の大赤斑などもそのようにして生まれた。イリヤ・プリゴジンが「散逸構造が生む秩序」と名づけた秩序もこれにあたる。そこでは系の物質とエネルギーの流動が秩序を生み出す新たな推進力になっている。
　このような特色をすべて兼ね備えているものがある。むろんのこと、それこそが「生物」すなわち「生︲情報系」なのである。生物システムは太陽のたえまない放射熱の流動によって駆動している散逸構造であり、物質代謝をおこないつつ秩序を生成する渦巻になっている。細胞は非平衡状態に生じた散逸構造そのものだ。
　
　秩序を生み出す系として、低エネルギーの平衡状態と、物質やエネルギーを出入りさせている散逸構造的な非平衡状態とがありうることを見た。それでは、これらに共通する秩序生成理論をくみたてられれば、われわれは生物進化に関する新たな基本法則に立ち会えることになるのだろうかというと、そうは問屋が卸さない。そこには主として３つの問題が待ち受けている。
　その３つの問題は、それら自身が自然の謎を解くときの基本法則に深くかかわっているため、新たな基本法則をたてるには、この３つの問題との関連をクリアしなければならない。すなわち、第一に量子力学との関連、第二にカオス理論との関連、第三にコンピュータとの関連である。

　第一の量子力学との関連の問題とは、分子レベルの現象に関する予測をするには量子力学を必要とするのだが、そこで見えてくる量子サイコロの目は生物システムの秩序を決定づけるには数が多すぎる。生物は分子現象なのである。そうだとすれば量子力学が要請する問題を進化論も引き受けなければならない。
　第二のカオス理論との関連の問題は、生物に古典的な決定論が成り立っていたとしても、初期条件のわずかな変化がのちのちの結果を変えるのだから、生物システムのどこにカオスが生じるかを見極めなければならないという問題だ。第１０６６夜のキャスティ『複雑性とパラドックス』で話題にしておいた。
　第三のコンピュータに関連する問題とは、コンピュータというものはそもそもチューリング・マシンを拡張したもので、そのチューリング・マシンは非平衡系の資格を備えているのだから、基本法則を構築するためにコンピュータを使用すること自体に難問が出てくるということを意味する。実はコンピュータが計算を実行できるのは、コンピュータが定常的なエネルギー源（電気）につながれ、そのエネルギーを消費しながらシリコンチップ上に電子的ビット・パターンを操作できるように構築されているからなのである。
　そうであるなら、コンピュータは「非平衡のアルゴリズム」であり、生物システムは「非平衡のコンピュータ」だということになる。カオスや複雑系の問題はその計算量が莫大になるために、コンピュータを除いては思考できないという宿命をもっている。だとすると生命とカオスの問題を解くにも、同時にコンピュータのアルゴリズムと生物のアルゴリズムをどこかで帳合をつけなければならないのである。

　この３つの難問が、生物現象にひそむ基本法則をあきらかにしようとする行く手に立ちはだかっていた。そこでカウフマンはこれらを点検しつつ、なんらかのブレークスルーの発見に立ち向かったのだ。キーワードは「自己組織化」「自己触媒」「自己創発」の三点セットだ。ブレークスルーの見込みは、それらがおこるのはきっと「カオスの縁」の近辺であろうという見当にあった。

21種類の分子から成り立つ自己触媒系のモデル
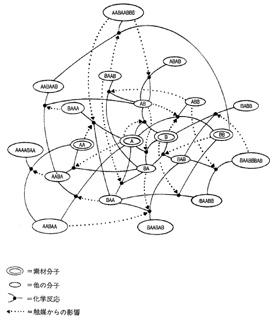
触媒作用を営む閉じた集団そのものが「結晶化」する

　カウフマンの仮説は、生物が集団的な自己触媒系になっているのであろうというところから始まる。生命は単一分子の性質の上に成り立っているのではなく、互いに作用しあう分子系の集団的な性質を前提に成り立ってきたというものだ。いいかえれば、生命は部分の加算の上に成り立つのではなく、部分と部分が相互作用する関係の集団的な創発性によって駆動したのだろうということだ。
　生物が見せる秩序で最も劇的なものはサケやセミやシマウマやヒトの個体発生であろう。ヒトでは一個の受精卵が５０回ほどの細胞分裂をくりかえして６０兆個もの細胞をつくりだし、受精卵では細胞の「母型」は１つだったのに、成体に向かうにしたがって２６０種類ほどの細胞の「子型」（神経細胞、赤血球、腺細胞、筋細胞など）を分化させる。「地の型」が「図の型」をつくりだすという驚くべきマジックだ。
　一個一個の細胞の中のゲノム（遺伝子のセット）はまったく同じなのである。それが発生分化するうちに異なる細胞になっていくのは、ゲノムの中で活性化する組み合わせが変わるために、さまざまな酵素やタンパク質がそれぞれ独自にできあがっているからである。こうして赤血球はヘモグロビンを、筋細胞はアクチンとミオシンをもつ。ということはＤＮＡとＲＮＡとタンパク質のあいだにはきっと複雑なネットワークが連絡しあっているはずなのだ。

細胞の交通
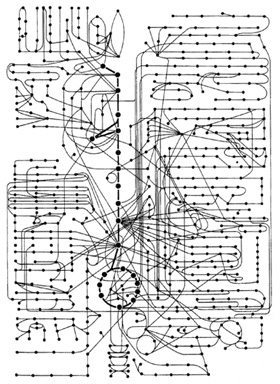
ヒトの中間物質代謝において、７００ほどの分子が相互作用する

　ドーキンスらのネオダーウィニズムでは、個体に秩序が生じるのは遺伝子がもつ分子機械の精密なはたらきによると考えられている。カウフマンはそうではなくて、個体発生に見られる秩序のほとんどは細胞レベルの複雑なネットワークのあいだに生じる自発的なもので、そこでは自己組織化がおこっているのだと見る。
　そこでカウフマンは、ネオダーウィニズムが「生物進化は遺伝子の利己性を維持するという有償行為を遺伝子に保証している」と強調するのに対して、このような自己組織化は「無償」であることをあえて強調した。劇的な個体の発生は、調節的なゲノムのネットワークが自己組織化をおこすことによって提供された「無償の秩序」だというのだ。自己創発だというのだ。
　ぼくは「無償の秩序」という言い方は当たっていないような気がするが（なぜなら第７０１夜に書いたように、細胞には細胞間のコミュニケーションがもたらす報酬系がはたらいていると考えるので）、それはこのさいおくとして、進化や分化の原動力が細胞のはたらきの周辺にあるだろうことに同意する。
　その「細胞のはたらきの周辺」とはどの周辺のことなのか。調べてみると、個体発生を促すゲノムのネットワークは「凍結した秩序の状態」「気体的なカオスの状態」「秩序とカオスのあいだにある液体的な状態」の３つの状態におこっているだろうということが見えてきた。カウフマンは共同研究者とともに、このうちの三番目に狙いをつけた。そしてその周辺を「カオスの縁」（edge of chaos）とよぶことにした。秩序と意外性が出会うところ、科学の言葉でいえばそこで相転移がおこるところが「カオスの縁」である。
　こうしてカウフマンは「カオスの縁」の研究にのめりこむ。折しもパー・バク、チャオ・タン、クルト・ウィーゼンフェルドらの「自己組織化臨界現象」にまつわる研究成果が次々に発表されていた。

　テーブルの上に砂山をつくる。その砂山にゆっくりと砂を加えていく。砂は積み重なって山になり、しばらくすると雪崩がおこって、しだいに形をつくっていく。大きな雪崩はめったにおこらない。小さな雪崩は頻繁におこる。やがてそれ以上何度にわたって砂を加えても、その姿をあまり変えない砂山ができあがる。これが「自己組織化臨界現象」のわかりやすい例だ。
　生命も自己組織化の途中でこのような臨界現象に達したにちがいない。それを「相転移」といってもいいし、また「自己触媒作用」だといってもいいだろう。いずれにしてもそのような相転移的な臨界現象はきっと「カオスの縁」でおこるはずなのだ。カウフマンはおおむねそのように仮説して、生物進化の秘密を握っているのは「カオスの縁」だと考えるようになった。
　
　かつて生命の発生や分化をめぐっては「ニワトリが先か、タマゴが先か」という議論が長らくつきまとっていた。第５９８夜に書いたアントワーヌ・ダンシャンの議論もそこにあった。これはずばりいえば「核酸が先か、タンパク質が先か」という議論であって、また、これをいいかえれば「情報が先か、機能が先か」という問題であった。
　この難問の突破口はなかなか見つからなかった。機能は情報がなければ組織化されえず、情報は機能を通してその意味を発現すると考えたくなるからだ。しかし、このように情報と機能の因果関係を閉じた輪にしてしまうと、もはや最初にあった発端はわからなくなる。
　それでも議論はしだいに明確になっていった。その端緒をひらいたのはマンフレート・アイゲンらであった。ハイパーサイクル仮説を展いた。『自然と遊戯』（東京化学同人）に詳しい。アイゲンはこう書いた、「このような自己撞着する問題を突破するには、分子系の自己組織化の理論をもってくるしかあるまい」。
　アイゲンが構想した自己組織化とは、「最初は無秩序な現象しかないとおもわれた系で、ある無秩序な現象の結果がその出発点にフィードバックして、ある種の増幅された動作を生み、それが適当な外部条件のもとで巨視的な機能的組織体にまで成長する」という現象のことをいう。
　きわめてわかりやすい定義というべきものだが、いまとなるとこの説明は地味すぎる。少なくともカウフマンの定義では、自己組織化は「カオスの縁」で相転移をおこす自己触媒作用なのである。

ブール代数的ネットワークにおける秩序領域、カオスの縁、カオス領域の模式図

ブール代数的ネットワークは、N個の二進法的、すなわちブール代数的遺伝子（活性である(=1)か不活性である(=0)かのどちらかの状態をとる）からなる遺伝子ネットワークのモデル。この模式図では、オン・オフする遺伝子が二次元の正方格子に並べられており、それぞれの遺伝子が四つの隣り合った遺伝子から入力を受けるようになっている。ｂ）のカオスの縁領域では、オン・オフと点滅する遺伝子の大小の島のようなかたまりへとばらばらになった状態にある。

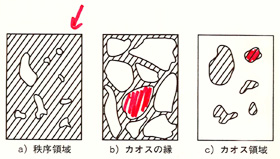
　本書ではこうした自己組織化をめぐるさまざまな議論が点検されている。その点検には互いに矛盾しあったり、互いに補完しあったり、同じことを別々の言い方にしていることなども含まれてはいるが、それでもなお、カウフマンは次の４つの基本法則の候補を提案するところまでたどりついた。
　候補の第一は、細胞を分子で構成された並列処理をおこなう動的システムだとみなすことである。そこにはブール代数的なネットワークが複雑に動いている。実際にそのような計算をしてみると、細胞の分子の状態空間に秩序領域とカオス領域ができているのがわかる。そして分子のネットワークは「カオスの縁」の付近で秩序をつくりだすことが見てとれる。まあ、ありそうなことだろう。
　第二の候補は、自己組織化によっておこる臨界現象を、共同体の集合がピークになっていると解釈することにある。なるほど、可能性のある見方だ。これはさきほどの砂山の例で説明した自己組織化臨界現象が細胞の集合にもあてはまることをあらわしている。だとすると細胞の共同体はそこで満員になり、それ以上に事態がすすむと局所的な絶滅がおこるにちがいない。
　第三に、第一と第二の法則が成立するなら、このような自己組織化現象では、細胞たちが適応地形を求めて「共構築」あるいは「共進化」しているとみなしてもいいだろうということだ。これはダーウィンの漸進説を精密に説明する法則になろう。
　すなわち、突然変異・組み替え・自然選択という遺伝的探索機構にもとづく進化のプロセスは、高地アルプスのようにピークが互いにかたまりあって裾野が適度になめらかであるような適応地形でないと成立しなかったはずなのだ。いいかえれば、生物圏というものが生命体と一緒に共進化しないかぎり、ダーウィンの漸進説は成立しないはずなのである。カウフマンはこの説明のために「ＮＫモデル」というものを導入するのだが、その有効性についての説明はあまりに技術的なので省くことにする（ＮＫモデルは「Ｎ個の遺伝子」と「Ｋ個の他の遺伝子の対立因子」から適応度を算出する方法をいう）。

　候補第四は、共進化する生物圏の動向には、いまだ科学が明示しえない「熱力学の第四法則」のようなものがあてはまっているのではないかということだ。カウフマンは、この幻の第四法則があきらかになれば、生物がつねに隣接可能領域をめざして進化してきたドラマを最後に説明するものになると考えている。
　第四の法則の期待については、生物たちが所属した化学的多様性からたえず隣接可能な化学的多様性に向かって進化してきたこと、そこにはどの分子も二基質二生成物反応がおこっていたこと、その可能性はおそらく生物システムの化学物質の多様性の二乗をめがけていただろうこと、そうだとすればそれが六Ｎ次元位相空間の出来事として語れるだろうといったこと以外には、まことにあやふやな予想しかしていない。
　ぼくとしては、その気持ちはよくわかるというふうにしか対応できないが、しかし、生物が４０億年近い時間をへて、いまなおこのように共進化してきたままにあるということを考えると、ここにはダーウィンの「穏やかな堤」をめざして共進化を成立させてきた「共構築」に関するなんらかの熱力学的化学反応的な法則がはたらいていたと考えたくなるのは当然のようにもおもえるのである。

相転移曲面の、細胞集団や組織への一般化

それぞれの細胞は、単独では一遺伝子あたりK個の入力をもっているが、Ｃ個の他の細胞と相互作用し、遺伝子生成物のうちｒ= Ｓ／Ｎの割合を細胞間で交換している。細胞集団や組織は、ＣやＳ／Ｎや、一遺伝子あたりの疎通入力を多くするようなバイアスを調整することで、相転移曲面上か、秩序領域内でそれに近い場所に位置するようになるとカウフマンは推測した。

　カウフマンが最後に到達したのは、自己組織化には「候補の法則」があるということだった。こんな科学用語はまだ認められていないものであるが、生物が進化してきた謎に答えるには、こういう法則を想定するしかないだろうという。
　自己触媒作用をしている細胞の共同体があって、それがモデルとなって「カオスの縁」を前後する臨界値を求めあう化学進化ドラマがあったということなのである。そのドラマを自然淘汰とよばないで「候補の法則」とか「候補の化学」とよんだのがカウフマンの自慢であった。
　今後、複雑系の科学がどう発展し、どう変化していくのかはわからない。まだ第二コーナーをまわったくらいなのではないかともおもう。Ｍ理論などの量子重力理論の充実によって大きく変更を迫られるかもしれないし、トポロジーやカタストロフィ理論がかつて果たした役割に匹敵する何かの仮説が実証されて、複雑系の全貌に新たな解読がもたらされるかもしれない。
　ぼくとしては、このあと数年ほどは放っておくつもりだ。やや理屈に勝ちすぎているのかなというきらいも感じるからである。