複雑性とパラドックス

　読書には灼熱に身をよじりたくなるような読書と、その灼熱をいったん避けて冷房の効く喫茶店に入って氷入りのアイスコーヒーを飲むような読書とがある。「気分を熱する読書」と「自分を冷やす読書」とがある。
　年間２億円程度の予算のサンタフェ研究所がジョージ・コーワンやマレー・ゲルマンを設立所長に「複雑系」（complex system）の理論をひっさげて登場してきたときは、世界が沸いた。その仮説には頓挫したものもあったけれども（頓挫なんて気にすることはないが）、刺激に富んだ構想とアイディアが目白押しだった。
　多彩な研究者たちはそれぞれの出自や所属をこえてサンタフェ研究所に招かれ立ち寄って、複雑適応系のための科学の樹立に推理と熱情をふりそそいだ。こうして、クリス・ラングトンやノーマン・パッカードによる「カオスの縁」の重要性の提起、パー・バクの砂山モデル論、トム・レイの人工生命「ティエラ」の実験、それらを体系的理論に組み立てていったスチュアート・カウフマンの勇ましい自己組織化仮説、ブライアン・アーサーの複雑系理論の経済学への適用、バーナード・デリダらのカオス的ネットワーク仮説、リチャード・バグリとドイン・ファーマーの自己触媒系の研究などなどのメニューが、「複雑系」の名のもとにふんだんに取り揃えられていったのである。
　さっそくこれらの成果を告げる何冊かにたてつづけに目を通したものだったが、それはほどほどに「熱する読書」というものだった。
　
　日本でも複雑系の議論は沸騰した。ぼくには金子邦彦・津田一郎・池上高志・合原一幸らのカオスの研究者たちの成果がめざましくおもえたが、経済畑やジャーナリズムはＩＴ産業の勃興を前にして経済学者ブライアン・アーサーの「収穫逓増」（increasing returns）をめぐる仮説をおおいに歓迎していた。
　ふつう、市場で成功した製品や企業はいずれは頭打ちになると考えられている。農産物や漁獲物を想定すればわかりやすいだろうが、おいしい米やおいしいサンマはいくらでも需要がある。けれども収穫しすぎた米やサンマは価格を下げていく。成功は長続きはしない。また成功した製品や企業は必ず他から真似される。真似されるほどのものでなければ市場を制することもできない。しかしこのことが過当競争を相互に煽って、いずれはやはり頭打ちになる。
　このように見るのが１００年前の近代経済学の巨人アルフレッド・マーシャルが定式化した「収穫逓減の法則」だ。そこには自由市場におけるアダム・スミスの「見えざる手」がちゃんとはたらいている。だから、この法則はたいていの経済現象や市場現象にぴったりあてはまっていた――かのように見えていた。
　ところが、ブライアン・アーサーの複雑系経済学が言い出したのはまったく逆のことだった。情報産業・ＩＴ産業・サービス産業では、しばしば最初に市場を制した“初物”がその後も勝ちつづけることのほうがおこりやすいというのだ。「収穫逓増の仮説」である。技術投資において先頭を走った者のほうが次々に追随者を吸収して勝ちパターンを強化するし、増産すればするほどコストも楽になるというのだ。マイクロソフトがそのいい例だという理論だった。
　この理論は需要と供給の「均衡」ではなく、市場の「不安定さ」に注目して、その不安定が特定企業や特定製品の増産と増収のカーブに周囲の流れを次々に巻きこんでいくとみなしていた。増加が増加を生む理論なのだ。
　仮説はまことに粗雑に流行した。「複雑系の経済学」「自己組織化する企業」「創発する電子製品」といった言葉が乱れとび、ＩＴベンチャーがそれならというので先陣争いに走っていった。なにしろ先手必勝の増加が増加を生むのなら、ＩＴベンチャーは一気に株式公開上場をしたほうがいい。Ｍ＆Ａもしてもらいやすい。ベンチャー・ファンドもこの仮説を信じてぶんぶん投資した。これが噂が噂をよんで、一挙に巨万の富を得る青年たちが登場していった。
　しかし、以上のような流行は必ずしも「複雑系の科学」の充実を告げるものではなかった。実際にもＩＴバブルはあっけなく崩壊してしまったのだし、カオスの科学や創発の意義を理解できている企業家も少なかった。複雑系の科学はフクザツなだけに腰を据えて考えなければならないのである。
　
　本書はウィーン工科大学の数理科学者で、サンタフェ研究所のジョン・キャスティが著した。複雑系の科学が孕むいくつものパラドックスをうまく説明した。
　本書を紹介する気になったのは、前著や前々著の『パラダイムの迷宮』（白揚社）、『２０世紀を動かした五つの大定理』（講談社）がすこぶる明眸だったので、それにつられて本書も読んでみたところ、類書にはない検討が加えられていて（たとえばシュレーディンガーの波動関数やゲーデルの定理やルネ・トムのカタストロフィ理論との関係など）、これなら複雑系の科学のやや高めの入門にはふさわしいと感じられたとともに、けっこうな「冷やす読書」ができたからである。たとえば、そのころはまだ複雑系の幾何学だという幻想をもって眺められていたフラクタル理論やマンデルブロ集合などを一刀両断のもとに切り捨てていた。これならサンタフェ・ブームに巻きこまれたアタマを冷やすのにもよいだろう。
　もっとも、本書の内容をもろに案内しても、さまざまな前提知識がないとわかりにくいかもしれない。そこで今夜は複雑系のフクザツなところではなくて、ザツなところから話してみたい。

　当初、複雑系というのは静的で安定な状態である系ではなく、乱雑で動的なランダムな系でもなく、そのあいだにあって時間の進捗にしたがって秩序やパターンを形成する系のことだとみなされていた。これでとくにまちがいだというのではないのだが、その後、複雑系を数学的な視点（オートマトンと数学という視点）でチェックしてみると、もうちょっと厳密に規定できることが見えてきた。
　自然界や世の中の現象をパターンのあらわれかたでみると、数学的にはだいたい次の５つの状態に分類することができる。
　第一の状態は均衡状態のように均一で変化がない（これがかつての需要と供給による市場理論にあたる）。第二の状態は景気循環のように周期的に変わりつづける（しかしなぜそのような周期になるかはなかなかつかめない）。第三の状態ではいつのまにか秩序のようなものが出現している（これはプリゴジンの散逸構造論が示したように、生命の分化や進化の謎解きの鍵になっていった）。第四の状態では次の予測がまったくつかないカオスが出てくる（そのカオスは初期条件の僅かな差異に発していた）。そして第五の状態が複雑系なのである。
　これはかなり割り切った区分で、数学者は好むけれども、物理学者や生物学者たちはこの区分はきれいすぎて、なかなかそうは問屋が卸さないとおもっている。それに、しばらくたってからのことだが、第五の複雑系は第三と第四の状態のあいだに隠れるように入りこんでいるともくされるようにもなった。これが複雑系のふるまいが「カオスの縁」に出てくると考えられるようになった理由なのだが、最初のうちは、カオスも複雑系も、いったいどうしてこのような数学モデルの途中にあらわれてくるのかは見当がつかないままだったのである。
　
　もうすこし別の見方で自然界や世の中の現象にきわだっている特徴を説明しておきたい。この特徴は生物には顕著なはたらきで、フィードバックには２つあるというものだ。「負のフィードバック」と「正のフィードバック」とよばれる。
　「負のフィードバック」はホメオスタシスに代表される作用で、体温や糖やホルモンの量を自己調節する機能をいう。暑ければ発汗し、寒ければ鳥肌をたてるのが「負のフィードバック」である。系が元のセットポイントから外れると、それを元に戻そうとする作用をさす。エアコンの自動調節機能についているサーモスタットがその簡単な原理をいかしている。「守りの作用」といえる。一方、生物にはこれとはまったく対照的に、あえて外部環境の変化にあわせて自分をどんどん切り替えていってしまう機能もある。これが「正のフィードバック」で、元から外れたら、その外れぐあいをどんどん大きくしてしまうという作用をいう。いわば「攻めの作用」にあたる。
　進化はおおまかにいえば、「正の攻め」によって進んで、「負の守り」に入って定着していった。生物全体の進化戦略からいえば、２つのシナリオをうまく配合したといっていいだろう。また、こうもいえる。生物たちは、「徹底してムダを省く戦略」と「ムダを捨てないで蓄える戦略」の２つを適宜くみあわせた。ウイルスはムダを省いた頂点にいて、ヒトはムダを蓄えた頂点にいる。
　これらのことは必ずしも複雑系の本質ではないが、生物がこうした両極の戦略シナリオのあいだにいるということが重要なのである。
　ちなみにブライアン・アーサーのいう「収穫逓増の経済学」は増加が増加を生むという「正のフィードバック」だけを強調しすぎた仮説であった。そういう可能性もありうるのだが（政府のインフラ提供などによる公共投資や勝ち目のある戦争投資など）、他方、「正のフィードバック」にはスピーカーの音がマイクに入ってハウリングがおこるというような、自己代入現象や自己再帰現象もあることを勘定に入れておかなければならない。ＩＴバブルの崩壊はＩＴ産業的ハウリングの結末だった。

　さらにもうひとつ、いまの話と似ているのだが、やや異なる視点からのフクザツな複雑系にまつわる特徴を話しておく。
　株価や為替の相場はつねに変動している。その変動はつねに大きな変動があるというのではなく、小さな変化がいろいろあって、ときにブラックマンデーのような大きな変動がどかんとやってくる。これは地震に似ている。地震も大きな地震がしょっちゅうおこっているわけではなく、小さな地震がビリビリとたえずおこっていて、それがあるときにチリや阪神淡路のような巨大地震につながっていく。活断層という不安定な系に何かがトリガーを与えたのである。
　この小さな変動のほうを「ゆらぎ」（fluctuation）とよぶ。もし株価の大変動や大地震を予測しようというのなら、ふだんどのようにこうした「ゆらぎ」がおこっているかということを、そのサイズ、振動性、頻度などを調べて分布をとっておくべきである。こういう分布を「指数分布」というのだが、この指数分布のグラフを観察してみると、株価にも地震にも似たような傾向があることがわかってきた。そこにはたいてい「相転移」がおこっていたのだ。
　水が氷になり、氷が水になるような現象が「相転移」（phase transition）である。水という　相が氷という見違えるような相に転移（transition）するとき、この現象を細密に観察すると、複雑系の一端が見えてくる。
　氷に温度を加えていけば水になる。氷は分子がガチガチになった状態、水は分子が自由に動きまわれる状態だ。この現象をミクロで見ると、氷が溶け出して零度に近くなっていくときは、水の分子がガチガチなものから急になめらかになるのではなくて、部分的に水になったり氷になったりしている状態があることがわかる。これが「ゆらぎ」（フラクチエーション）である。「ゆらぎ」は零度になる前ではまた消えて、氷に戻ってしまうということをくりかえす。ところが事態が零度にうんと近づくと、「ゆらぎ」は元に戻らずに、水の分子が自由に動きまわれるようになる。これが「相転移」である。相転移がおこる付近では、水の領域（水になろうとする可能性）と氷の領域（氷になろうとする可能性）とが鎬をけずりあう。こういう場面を科学では臨界状態という。
　相転移は臨界状態の間際でおこる。実例はいろいろある。水が水蒸気になるのも相転移だし、ブリキ板やプラスチック板をぐうっと曲げつづけるとあるところでバキッと折れてしまう座屈も相転移だし、磁力をもっている鉄を熱していくとあるところで突然に磁力がなくなってしまうのも、鉄の臨界状態でおこった相転移なのだ。
　
　物質が相転移をおこすふるまいはいろいろである。その示し方は、オーダーパラメータ（秩序変数）とよばれる量がその系の臨界状態の付近で急激に変化することをあらわす数学で記述される。
　氷が水になり鉄の磁力がなくなるような臨界状態や相転移は、外部から熱を加えて生じたことであって、システムの内部で勝手におこったわけではない。ところが大地震のような現象は、外からのはたらきかけというより、小さな「ゆらぎ」が臨界状態をつくりだしたためにおこる。
　こういうふうに、システムが自分で臨界値に達して相転移をおこしているばあいを「自己組織的な臨界現象」という。チリや阪神淡路の大地震のトリガーになったのはこの内部的な臨界現象だった。外のトリガーではなかった。これは自己組織的な臨界現象、略して「自己組織化」（self-organization）のせいである。

　自己組織化という用語は自分で自分の新たな秩序をつくりだしていくことを示している。生物はすべて自己組織化的な臨界状態を自分でつくりだして相転移をおこしていると考えられる。朝顔が朝咲くようになったのも、サナギが蝶になるのも、神経系のネットワークができたのも、白血球やＴ細胞ができたのも、みんな自己組織化による相転移のせいだった。そこには要素の組み合わせからだけでは予想もつかない秩序がつくりだされている。
　ただしそのしくみを説明しきることはなかなか容易ではない。とくに細胞の自己組織化はいまなお数学で記述できないほど複雑な相転移をおこしている。
　生物だけではない。空気や液体の流れも自己組織化をおこすし（たとえばベナール対流）、ハリケーンも台風も自己組織化をおこしている。レーザーも自己組織化をおこすし、まだ研究されていないけれど、能管のような笛の音にもすばらしい歌声にも自己組織化がおこっているとみなされる。プリゴジンは熱力学的に非平衡な系ではこうした自己組織化はしょっちゅうおこりうることを示した。非線形現象のひとつのソリトンを案内した第八四八夜やプリゴジンの熱力学を紹介した９０９夜などを参照してほしい。
　いったい、こうした相転移や自己組織化や臨界現象の奥に共通している現象は何なのか。それを複雑性というのなら、そのフクザツ度とはどういうものなのか。
　
　そこでカオス（chaos）の話になる。
　カオスは微分方程式を解いているうちに発見された。たとえばニュートンの運動方程式がその代表的な例なのだが、そうした微分方程式は最初に初期条件を入れれば、その方程式に何を代入してもその後の物質の運動は計算結果ですべて決まってくる。答えが時間の経過につれてばらついたり、振動したりすることはない。数学ではこれを「決定論」（determinism）という。
　ところが１９７０年代の後半あたりからコンピュータでものすごい計算ができるようになると、こうした決定論的な方程式の計算結果にばらつきが見えるようになった。初期値が一定なのに計算結果にばらつきや振動や分裂がおこることが見えてきた。これがカオスだった。カオスはでたらめやランダムネスや無秩序なのではない。カオスは決定論という一定のルールのもとに、何か特異なふるまいをもつ変化としてあらわれる。このようなカオスを「決定論的カオス」という。
　決定論的カオスは一部ではもっと以前から知られていた。１９６３年に気象学者のエドワード・ローレンツは「ちょっとコーヒーブレイクをしているあいだ」に、とんでもない結末を知る。
　ローレンツは気象を決める三つのパラメータ（自由度）を用いて非線形の微分方程式を大型コンピュータで解こうとしていた。３つのパラメータは温度・気圧・風の方向だ。最初はこれらに６桁の数値を入れて（実際の入力数値は０.５０６１２７）、ついで検算のときは四捨五入して三桁の数値で計算を始めた（入力数値は０.５０６）。
　コンピュータは黙々と計算をしつづける。ローレンツがコーヒーブレイクのために席を立って戻ってきてみると、とんでもない計算結果がディスプレーされていた。１０００分の１未満だった初期値の誤差が方程式を解いているうちに途方もなく増幅されてしまったのだ。信じがたい「正のフィードバック」がおこったようだった。
　ローレンツはこうなった原因が、非線形という方程式の性質と代入をくりかえしているという数学的行為によっておこったことに気がついた（ローレンツがこのとき使用した数式が流体力学の基本方程式であるナヴィエ・ストークス方程式である）。非線形な数式とは、ここでは「結果が原因に比例しない数式」と考えればいい。もうすこし厳密にいえば「出力が入力に比例しない関係をあらわす数式」というふうに解釈できる。

ローレンツ・アトラクター

　ローレンツの計算が示したことで重要なのは、カオスは「初期値に敏感な依存性」にかかわっていることにある。カオスは初期条件にセンシティブなのである。
　これはその系（システム）が不安定であることをあらわしていた。不安定ということは、将来の予測がつきにくいということで、その正体が初期値のちょっとしたズレ（誤差）であらわれてくる。ローレンツはこのことを、「バタフライ効果」と名付けた。北京でひらひらと飛ぶ一匹の蝶々の効果がまわりまわってシカゴ（ニューヨークでもいいが）に嵐をもたらすという比喩だ。カオスが初期値に敏感だというのは、この蝶々のひらひらに依存する動向が後々になってあらわれるという意味だ。
　カオスはいわば「前途を知らないシステムにおこる特異な現象」なのである。カオスはバタフライ効果が後日にやってくるものなのだ。
　そうだとすれば、カオスは相転移や自己組織化をおこすシステムのどこかに生じていると考えたくなる。察するに、相転移や自己組織化も「前途を知らないシステム」に見える。もっとはっきりいえば、カオスが生じている局面の前後で相転移や自己組織化がおこっているのかもしれない。バタフライ効果が如実になってくるところで、複雑度やカオスや相転移がおこっているのかもしれない。ということは、カオスは複雑系の特質をつくっている要因のひとつ、それもきわめて重大な要因なのかもしれないのである。
　こうして、カオスがどこでどのように生じているかを研究することこそ、複雑系のシステムの本質の解明につながるのではないかというふうに考えられるようになってきた。
　
　学習やファッションや組織経営にＴＰＯがあるように、カオスにもＴＰＯがある。Ｔ（時間）についてはカオスが時間の経過によって生じることがわかっている。時間がたつにつれカオスの相貌は変化する。それゆえカオスは「タイミングを見はからっている現象」だともいえる。
　Ｐ（場所）については、カオスは場所が適切なところでないと生じないことが知られている。「カオスは場所を選択する」といってよい。ここに複雑系の研究者たちが重視した「カオスの縁」がかかわってくる。カオスが出現するところ、その周辺や縁、そこに複雑系をフクザツにしている何か特別な作用がはたらくと想定される。Ｏ（場合）についてはいろいろの見方ができる。カオスがどのようなオケージョンをとらえているかが判然としないからである。カオスが偶然性のほうに属しているのか、必然性のほうに属しているのかの峻別もつきにくい。
　山口昌哉は名著『カオスとフラクタル』（講談社ブルーバックス→ちくま学芸文庫）のなかで、「カオスはある種の偶然性が必然性と近づく場面を、必然性の側から眺めたもの」と説明した。うまい説明だが、これはひとつには、カオスが実験やコンピュータ計算のなかから生まれているという特色が目立つためである。ただしこれでは偶然なのか必然なのかは決めがたい。カオスのＯは計算途中に秘められていたのである。
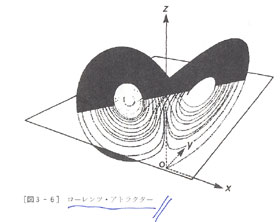
　カオスはシステムのなかで独自のＴＰＯをもつふるまいをする。そのふるまいは、基本的にはアトラクター（attractor）というものでわかる。
　
　アトラクターは字義通りの「何かを引きつけるもの」であって、かつ「何かに引きつけられるもの」である。
　そういうアトラクターに注目すると、ある座標（相空間＝多次元多様体＝状態空間）の上での「点」の動きが時間の経過とともに軌道に吸い寄せられる状態をあらわせる。カオス研究がさかんになる前は、アトラクターとしては「平衡点」「リミットサイクル」「トーラス」がよく知られていた。
　平衡点は摩擦のある振子の運動が見せる軌道である。どんな初期状態からスタートしても最終的には静止状態に落ち着く。点アトラクターともよばれる。リミットサイクルは流体エネルギーや電気エネルギーや機械エネルギーによって止まることなく一定の周期を描いているアトラクターだ。振子時計や水晶時計の軌道、あるいは渦をもつ乱流などがこの状態にあたる。
　たとえば乱流は棒切れなどを入れてかきまわしても、流れはそれに影響されないで平気で元の運動をそのまましつづけるのだが、これを座標であらわしてみると円アトラクターになる。これがリミットサイクルだ。
　点アトラクターから円アトラクター（リミットサイクル）に変わるところはホップ分岐とよばれる。トーラスは概周期アトラクターあるいは準周期アトラクターである。２つのリミットサイクルが独立しながら連動するとトーラス（ドーナツ）型のアトラクターが生まれてくる。
　これらはアトラクターではあるけれど、いずれもカオスではなかった。ところが、新たに発見された「ストレンジ・アトラクター」はこれらとまったく異なって、リミットサイクルやトーラスとくらべると格段に複雑度が増していくことがわかった。しかも自由度（ここではパラメータの数と思ってもらえばいい）が２では、カオスは生まれない。ローレンツの非線形微分方程式が３つのパラメータをもっていたように、自由度３以上がカオス出現の条件なのである（ストレンジ・アトラクターはいまではカオス・アトラクターという名で呼ぶようになっている）。

ストレンジ・アトラクター

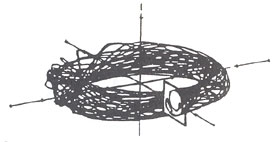
　ストレンジ・アトラクターは、リミットサイクルやトーラスに３つ目の自由度が加わっておこることが少なくない。リミットサイクルが壊れたり、トーラスが歪んだりぐちゃぐちゃになってストレンジ・アトラクターになる。
　このようなカオスをイメージするのは容易ではないが、二次元（自由度２）の一枚の紙をくしゃくしゃに丸めれば立体になり、その紙に描いてあった点や線が丸められた紙つぶてのなかでは意外な描線になることを想像してみればいいだろう。ただしここには大事な特色がある。ストレンジ・アトラクターは紙つぶてや糸玉のようなものだとはいえ、その軌道のループは二次元（平面）の上で隣どうしの軌道を近づけながら揃っていくのである。どんな軌道も二度と同じところをくりかえして動くことはない。これでわかるように、カオスは周期的なのではない。きわめて複雑な非周期的な動向なのだ。

　カオスの動向は多くの予測を裏切るもので、そこにはたいてい不安定という状態が待ちかまえている。しかし不安定であればこそ、カオスはそこを通り抜けるにあたって悩みぬいたすえ、決定論的な秩序を忘れずに複雑性というものを発揮していく。
　このことはいいかえれば、カオスはいわば創造の苦悩を背負った現象だというふうにもいえる。まさに複雑系の研究においてカオスが脚光を浴びてきたのは、この性質によっていた。
　ざっとこういう経緯の検討をあれこれ進めてきて、「複雑系の科学」というものが、正のフィードバック、相転移、自己組織化、バタフライ効果、不安定、ストレンジ・アトラクター、カオスといった現象を食べてきたのである。そんななかで、サンタフェ研究所では、とりわけ「カオスの縁」という概念が浮上した。複雑系の現象や動向は一言でいうならみんな「カオスの縁」でおこっているのではないかというのである。

システムの崩壊のカスプカタストロフィー・モデル

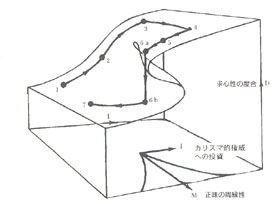
　こんなところで、フクザツな話のなかのザツな話の案内をおいて、以下は、これらのザツな話がどのように複雑系の本質とおぼしい問題とかかわっているかということと、本書『複雑性とパラドックス』の結論部分の紹介に入りたい。
　主要な研究者たちの見解をとびとびに集約しておこう。マレー・ゲルマンは「複雑適応系はパターンを追い求める。そのときにシステムは情報を書きこんでいく」と考えた。これは「複雑系はアトラクターをもつ」と結論づけているようなものだった。クリストファー・ラングトンは「複雑系は相転移によって形成される。その相転移はカオスの出現の直前に始まる」と考えた。「カオスの縁」にこそ複雑系の秘密があるという見解に広がっていったのはこのあとだ。ラングトンは『セルオートマトン』（共立出版）でも知られるように、最初はライフゲームによる複雑系としての生命進化の謎の解明に熱中していたのだが、スティーヴン・ウルフラムやノーマン・パッカードの研究に出会ってその謎が「カオスの縁」にありそうだということに気がついた。ラングトンは「人工生命」（Artificial Life）の命名者でもある。日本では池上高志がこの志を継いでいる。
　もっと本格的に「カオスの縁」にとりくんだのはコーネル大学のサイモン・レヴィンと共同研究をしていたスチュアート・カウフマンである。カウフマンは『秩序の起源』（未訳）を著して、適応度地形（フィットネス・ランドスケープ）というモデルをつかうことで複雑系における共進化という概念を浮き彫りにし、そこに自己組織化臨界現象の解法を求めた。それでどうなったかといえば、「共進化する系はおのずからカオスの縁に達する」というふうになった。かれらの見解は、こうである。「カオスの縁こそは計算機能が最大になる場所なのである」。
　こういうとびとびの要約をしていくと、サンタフェ研究所の成果を読むのはやっぱり「熱する読書」だということになるのだが、しかしジョン・キャスティはちょっと待ってくれと書いたのだ。ぼくもここから先は一気に「冷やす読書」のエッセンスをお目にかけたい。
　
　本書は「観察」の話から始まっている。観察そのものと観察の結果をモデルにすることの関係を問うたのだ。観察とモデルの関係は、観察の結果を測定値にしたとたんに微妙になってくる。
　これは現象（対象）と言葉の関係に似ている。ヴィトゲンシュタインは生涯にわたって言葉とそれがあらわす対象との関係に悩まされつづけた哲人であるが、その悩みは前半の思索と後半の思索が正反対になったということによくあらわれていた。ヴィトゲンシュタインは当初は、“言語の映像理論”とでもいうべきものを考えて、言葉による言明は一連の映像に対応しているはずだとみなして、言明が真か偽かは映像（さまざまな現実的な現象の構造や特色）を観察することによってしか証明できないと結論づけた。
　ところが後半になって、現実的な世界について言語は「語る」ことはできず、ただ「示す」ことしかできないと考えた。第８３３夜に書いたように、これはまさしく「カタルトシメス」（「語る」と「示す」の関係）をどう考えるかということだった。デヴィッド・ボームも「レオモード」（流態）を提案して、量子力学の現象を言葉であらわすにはどうすればよいか、腐心した。なぜそんなことにとりくんだかといえば、科学の言葉は主述の論理としてとっくに古典力学の領域でがっちり決められてしまっていたからだ。その同じ言葉で量子現象をあらわすのは、難しいというより、まちがいになりかねなかったのだ。
　ここで、複雑系は語りうるとみなせるのか、それとも示すだけにすべきかという問題が立ち上がる。いったい科学は複雑系の現実や現象を観察しているのか、それともそのモデルを作っているのかという問いである。
　
　アメリカの憲法の第５条は、憲法自体を修正するときの条件を定めている。それによると下院・上院双方の少なくとも３分の２の賛成があれば修正案は可決されるが、全州の４分の３の議会による追認を必要とするというふうになっている。では、この第５条そのものを修正するには、この規定に従っていればいいのだろうか。
　これは、他の規則の変更を規定している規則は、その規則自体の変更に対しても適用できるのかどうかを問うた問題で、「エンド・パラドックス」の問題といわれる。いいかえれば、システムの一部のルールを用いてシステムのルールそのものを変えることはできるかどうかという問題だ。
　ふつう、このような問題の背後には「全能性のパラドックス」が控えていると想定されている。クレタ人が「すべてのクレタ人はうそつきだ」と言ったことは真か偽かという、例のエピメニデスのパラドックスである。本書は、これを論理学の問題から計算の問題に移して、計算はどのような言述された対象（現象）に対応できるかという問題に設定しなおした。複雑系の科学は計算可能なものになっているのかどうかを問うたのだ。
　検討してみると、この問題に答えていたのはアラン・チューリングのチューリング・マシンだった。今日のコンピュータ（計算機械）の母型にあたる。

12状態チューリング・マシン

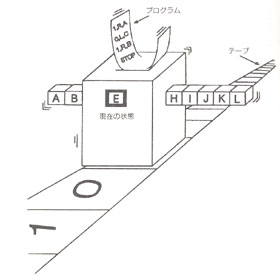
　チューリング・マシンによって、われわれは何かを計算するということのよく定義された概念モデルをもった。まさに天才的な計算モデルがすでに用意されたのだ。しかしそうだったとすればそれはそれで、今度は、われわれはいったい何を厳密に計算できるのかという問題が出てくる。たとえば「計算の範囲を超えた数」なんてものを対象にしてしまってはいないかとか、逆に「計算可能な数」はそもそも現実世界の何にあたるのかとか、そんな問題をかかえることになる。
　これは「計算可能性」という新たな問題であって、また、いつでも計算を停止すべき「停止問題」というものがあるかもしれないということを暗示する。さらには全能性のパラドックスではないが、計算の一部を計算の全体にあてはめるとどうなるかという、とんでもない問題を孕ませることにもなりかねない。
　こうして、ゲーデルの証明（不完全性定理）がこれらの問題に関与することになる。第１０５８夜であらかたのことを案内したのでここでは省略するが、ゲーデルはゲーデル数という奇妙な手続きを導入して、計算における決定不能性を導き出した。本書はこの証明の背後にある「数の複雑性」というとんでもない正体に立ち入って、グレゴリー・チャイティンの思索を借りつつ、「どんな数学の理論が証明できることよりも大きな複雑性をもつ数が存在する」ということを説明してみせていた。圧巻である。

論理空間におけるゲーデルの第1不完全定理

　ここまでで、キャスティが何を言いたかったかというと、カオス的な力学過程があることによって生じる複雑性は、チューリング・マシンやゲーデルの証明の問題と重なっているということ、もうすこしちゃんというなら、形式システムの定理とチューリング・マシンのアウトプットと力学系のアトラクター集合とは、ほぼ等価であるということである。これらのうちのどれかひとつが与えられれば、他のどれかへの翻訳が可能なのだ。
　これはカオスが真理もしくは創発性の秘密を握っているということを強く暗示する。すでに述べたように創発（emergence）とは、部分を足し算していくとその部分のどこにもなかった性質（創発特性）が、その系の全体としてあらわれることをいう。複雑性における創発性というのは、カオスをモデルと観察とのあいだで眺めるということそのものが創発性の源泉になるということだ。これを逆にいうのなら、ストレンジ・アトラクターやカオスのない世界は、数学モデルと観察とのあいだで、まことに貧弱な描像しかもてないだろうということになる。
　創発性の問題は難問である。そこには不完全性や還元不可能性が絡んでくる。キャスティはその難題にめげることなく挑んでいく。複雑系の科学が金科玉条にしている概念に挑みかかっていくのだ。いや、キャスティは複雑系の科学の反対演説をしているのではない。そうではなくて、複雑系の科学にはいくつもの「際」があって、その「際」を含まない複雑系の科学はなんであれ証明しようがないと言っているのだ。
　こうして本書の結論部分は、複雑性は本質的に主観的概念であるというふうになってくる。くだいていうのなら、複雑性は「真」「善」「美」のような、あるいは「悪」「罪」「神」のような、そのシステムに所属したものからしか見えてこないものだと結論づけたのだ。どうだろうか、「冷える読書」というのも、ときにきわめておもしろいものなのである。

　それでは、複雑系の科学を考えるときのごく一般的なまとめを書いておく。ざっとこんなふうになるだろうか。
　いろいろな要素が集まったシステムを考えるときの方法には、要素のふるまいを理解して、これをシステム全体に拡張するという線形的な方法と、要素間の相互作用から予測のつかない変化がおこったことに注目する非線形的な方法とがある。歴史的にはアリストテレス、デカルト、ホッブズ、アダム・スミスは線形的方法を駆使し、アンリ・ポアンカレによって初めて非線形的方法が使えるようになった。ベイトソンやボームらもここにつながっていく。
　複雑系とは、第一に相互作用が非線形であり、第二に物質やエネルギーの流れが開放されていて、そのため第三に、システムの内部で組織化がおこって、それが動的に変化するという特徴をもっているとみなせるシステムである。それゆえ複雑系の科学は非線形的方法の対象になる。しかし、もしそうだとするのなら、非線形方程式が複雑系のための唯一の数学であるかどうかが問われなければならない……。以上。

モデル関係