確率論的思考

　サッカーのワールドカップでブラジルが優勝するかどうかの確率を計算する。それまでのブラジルの勝率は７２パーセントで、そのまま決勝トーナメントに進出したとしよう。７２パーセントという勝率はかなり高い。プロ野球ならシーズンぶっちぎりだ。しかしブラジルが優勝できる確率はわずか２４パーセントにすぎない。決勝トーナメントで４回勝ちつづける確率とはそんなものなのだ。
　では、どのチームが優勝するかという確率はどうかというと、これはどう計算しようと、おっつかっつだ。ただし、ブラジル以外のチームが優勝する確率なら７６パーセントある。こうなると、ブラジルの優勝はかなりの偶然がかかわっていないと実現できないということになる。これはチームの実力の評価とは関係がない。優勝する確からしさを求める確率の話なのだ。確率はけっこう冷酷なものなのである。

　確率という言葉は、英語の“probability”を、明治４１年に東北帝国大学の林鶴一が訳した日本語だ。うまい訳だとは思うけれど、この意味をちゃんと受け取るのは容易ではない。プロバビリティの意味が、古代ローマのキケロの時代のプロバビリスこのかた、いろいろ広がってきたからだ。
　ラテン語のプロバビリスは、確かなことを求めて「検証する、立証する、証明する」という意味だった。そこからいろいろな意味が混成されてきた。たとえば、疑いないこと（sureness）、信頼できること（reliability）、確実なこと（certainty）、可能性があること（possibility）、ありそうなこと・もっともらしさ（likelihood）といった意味あいが、つまりはヨーロピアン・ロジックが好きそうな概念が、だんだん含まれるようになった。
　確率的な言葉にこれだけの意味あいがあるにもかかわらず、こうしたことすべてを、確率論ではまだ扱えてはいない。それをしようとすれば、そこには哲学や思想もかかわってくるし、自然科学とりわけ量子力学以降の物理学や遺伝子工学以降の生物学もかかわる。とくに認知科学は欠かせない。確率論もニューステージに向かう。
　それなのに、確率を儲けの武器やリスクの回避だけに応用するのは、無理がある。確率は「確実なこと」を決めるためのものというより、「不確かなこと」を確実だと見誤らないためのものであるからだ。

　われわれは不確実な社会のなかで暮らしている。あした事故に遇うかもしれないし、誰かから恋心を告白されるかもしれないし、次の一冊の読書が人生を変えるかもしれない。２０１０年の為替相場も、ドバイの経済動向も、日本の百貨店業界が景気を取り戻すかどうかも、ぼくの新刊本がどのくらい売れるかも不確実だ。
　これらをまとめて不確実性（uncertainty）というのだが、ここにもいっぱいの同義語や類義語が入り交じっている。「不確か、不確定、定かではない、はっきりしない」などは当然だとして、「曖昧、不鮮明、疑わしい、信憑性に欠ける」、あげくは「どっちつかず、中途半端、ぼけている、漠然」なんてものも入ってくる。
　不確実性はわかりにくいわけではない。「わかる」は「分ける・分かる・解る・判る」であって、これこれは不確実なことだろうというふうに情報や現象を「わける」によって「わかる」にしているのだから、不確実なことがわからないわけではなく、そのように「わかる確実」と「わかる不確実」を分けたのだ。
　それなら不確実性の性質を「起こりやすさ」から見ればどうなのか。つまり確率的に不確実なことを見るとどうなるか。そういう見方に変えてみると、不確実性とは「起こりやすさ」の予測ができないことで、当該の不確かな情報の制御ができないことを意味することになる。
　しかしあらためてよくよく考えてみると、こういう確率が生ずるのは自分が“そこ”にかかわろうとしたためなのだ。だからこそ予測ができなかったり、制御ができなかったりしたわけだ。放ったらかしにしておけば、なんであれ事態と自分の関係は「あるがまま」である。ところがおかしなことに、そこにかかわろうとして、その予想のなかの主人公になったとたんに“そこ”が確実か不確実かに分かれていく。

　どんな不確実なことにも、まったく予測のつかないこともあれば、多少は予測の範囲が見通せることもある。ぼくの死亡日はまったく予測がつかないが、ぼくが来年どんな本を書くかは予測の範囲がそこそこ見通せる。
　フランク・ナイトは前者を広義に扱って「不確実性」と呼び、後者を狭義に扱って「リスク」と呼んだ。リスクは予測の範囲が確率で示せるものをいう。ナイトの定義でいけば、確率の対象となる情報はすべてリスクなのである。つまりリスクは不確実性から突起したものなのだ。
　ぼくが来年に書く本はさまざまな度合いのリスクを含んでいて、ぼくが死ぬだろうということは確実な不確実なのである。リスクを確率的に予測し、リスク・マネジメントをしようとしたとたん、不確実性と確率とのあいだの不安と野望に、われわれはたちまち立ち会わされる。
　こういうことは、当事者にならなければわかりにくいことだ。ぼくは株の投資を一度もやったことがないし、金融関係の企画にかかわったこともないが、たとえば何かの仕事をしようとする場合、その意思決定者が自分であるとき、その仕事の不確実性と「確からしさ」の狭間に不安か自信かのどちらかを強くもちすぎた瞬間、余計なリスクのことを過剰に感じたり、過小にとらえすぎたりすることを、これまで何度も実感してきた。それが確率論にかかわっているとは、正直いって実感できていなかった。
　でも、最近は不確実すぎる社会がひたひた身に寄せてきて、それはそれで徒然草っぽくてけっこうじゃないかと思っていたのだが、そのうち、自分が過剰になるか過小になるかということと、さまざまなオプション選択に悩む日本の姿とがだぶってくると、これは確率論的哲学もけっこう必要なんだろうと思えてきたのである。

　本書で「確率論的思考」とよばれているものは、哲学ではない。不確実な世の中の不確かな現象のなかで、確率的に予測できそうなこととは何かを扱おうとしたときの柔らかい思考のことをさしている。
　ふつう、確率的に予測できそうなことは、そのことがおこる可能性はどのくらいあるかということだから、いくらでもありうると言えるだろうという気になるが、実はそうはいかない。それを確率の数値で示そうとしたとたんに、さまざまな可能性にも野望にも向かえる一方、思いがけない困難にも難関にもぶちあたる。たとえば明日の株価が上がるか下がるかなど、それこそ誰もが知りたいことだろうに、高度な確率式をどう使ったところで、とうてい予測がつくものではない。

　本書の著者は、日本長期信用銀行でデリバティブを利用した商品設計やポートフォリオ・マネジメントに従事したのち、海外証券子会社に出向してデリバティブ・ディーリングのデスクを務めた。その後、三菱ＵＦＪ投信のチーフファンドマネージャーとして、債券運用・フロントリスク管理・社債投資などに従事して、いまは名うての金融アナリストとしてひっぱりだこになっている。
　その著者が長年の金融市場から学んだ結論は、相場の先行きを正確に予測することは不可能であるだけでなく、そもそも正確に予想すること自体を避けるべきである、ということだった。

　著者の推奨する確率論的思考は「ものごとはできるかぎり長期的に見たほうがいい」ということにある。
　これはいいかえれば、不確実な世界のなかでは確実なことは急速には何も求められないということだ。そこにあるものは、かつてこの言葉をロバート・ルービンが使ったのだが、確率的にものごとを考えるのにふさわしいのは「蓋然的思考」（probabilistic thinking）だけなのである。ルービンはゴールドマン・サックスのトップに上り詰めたトレーダーで、その後は財務長官として辣腕をふるった男である。
　著者のいう確率論的思考も、この蓋然的思考の範囲のなかにある。ルービンとは違って、もっと柔らかい。それは、この著者がリスクに満ちた市場で仕事をしていながらも、リスクの回避は長期的な流れのなかでしか贖えないという見方をしているからだ。
　仏教的だとは言わない。達観でもない。本書にはそんなことを感じさせる文脈や引例は一言もない。けれども、最近の金融関係者も少しはこういう柔らかい発想をするようになったのかと思うと、昨今のリーマン・ショックや囂々たるネオリベ批判（ネオリベラリズム批判・新自由主義批判）のせいもあるだろうが、ややホッとする。
　まあ、それはそれとして、なぜ確率論を使っても蓋然的になったほうがいいか、少し考えてみたい。

　株価が上がるかどうかは、それをどう予想したかによって当たりぐあいが大幅に異なってくる。予想をしなければ、確率は生じない。
　たとえば「この銘柄の株価は上がるだろう」というような宣言なら、いつか上がったときに、ほれほれ当たっただろと言えばいいのだから、それですむ。問題は時期を限って数値を予想するときで、「１ヵ月後に株価は上がる」という予想なら５０パーセント程度の確率で当たるわけだが、「３ヵ月後に７パーセント上がる」となると、まず当たらない。そんなことができるトレーダーや経済学者は世の中には一人もいない。当たるときはただ「まぐれ」なのである。
　ところが、任意に選んだ１０社の銘柄が今後１０年間にどんな株価を示すのかといったことになると、確率はかなり雄弁な回答を用意する。実は最近のトレーダーやファンドマネージャーたちは、こちらのほうのことだけを確信しているにすぎない。
　なぜ特定の短期予測は不可能で、多様な動向を長期的にみることにはある程度の確信がもてるのだろうか。それなのに金融機関は世間に投資予測をまきちらして、短期の投資者を惑わせるのだろうか。
　こういうトレーダーたちの事情を知って、そいつはずるいじゃないかと思うか、そもそも確率的予測とはそういうものだと思うかが、統計的な見方や確率的な見方をするときの分かれ目になる。ぼくはマッドマネー資本主義にも一様な民営主義にも黄昏が訪れているのなら、後者のほうの見方をする金融関係者がもっとふえてこなければいかんだろうと思う。
　つまりは、確率論的思考とは、この分かれ目にフナドの神（分岐や三叉路の神）のいたずらが感じられるようになることなのである。それにはしかし、確率の愉快と不快の両方を実感できたほうがいいはずだ。

　確率とは、ある事象がおこりうる「確からしさ」をあらわそうとしたときの数値表現のことである。
　数学的確率は数学的な対称性を基本においている。どのように確率論を使うかというと、いくつかのモデルの選択がある。大きくみると、数学的確率、頻度主義、主観的確率、論理的確率の四種類がある。
　確率論の本には必ずうるさいほどサイコロやコインやカードの例が出てくるが、これは「サイコロで３の目が出る確率は１／６である」というやつで、ここではサイコロが立方体という六面の対称性があることを念頭においている。コインやカードは２面の対称性である。
　このようなときの「起こりやすさ」や「確からしさ」は、数学的に「場合の多さ」（場合の数）として表示され、出来事の場合の数が全体の何パーセントに当たっているかだけをあらわす。それゆえ数学的確率は、確率をはなはだ理想的で抽象的なものにして、人間のイデアの中に確率を鎮座させてきたとみなされても仕方がない。
　２つめの頻度主義による確率モデルは、統計データから確率を導きだす。注目している出来事がどのようにその現象のなかでおこっているかをデータとして引き出して、その出来事の頻度が占める割合を算出し、それを確率とする。ここでは「起こりやすさ」はデータの観測頻度なのである。このような頻度主義型の確率は、物理学や生物学のように実験をくりかえせるような例では、そうとう雄弁になる。洗濯機やジェットエンジンの故障は、この実験的確率によって減少させる。
　主観的確率は、文字通り、人間がそこにかかわったことによって生じる確率を計算しようとするものだ。端的にいえば、出来事の「起こりやすさ」や「確からしさ」そのものを確率の対象にするのではなく、そのことを“どう思っているか”を確率モデルに入れる。
　これをベイズ主義ともいうのだが、この確率論の長所と短所は「いいかげん」なところにある。主観的確率は「思いこみ」入りなのだから、客観的に正しい予測ではない。正しいかどうかということを、不確実な現象のなかで言明することも、またたいそう曖昧なものなのだ。「いいかげん」は「良い加減」でもあって、また「いい加減」でもある。主観的確率は加減三昧だった。
　４つめの論理的確率は、ＡならばＢであるというような論理学的な推論のうえに成り立たせようとする確率で、おおかたの論理哲学や、とりわけコンピュータのアルゴリズムにはうってつけである。とくに説明するまでもないだろう。

　ベイズ主義について一言加える。
　さきほども書いたように、主観的確率のモデルのプロトタイプは「ベイズの定理」にもとづいている。１８世紀の牧師で数学者でもあったトマス・ベイズによるものだ。
　これは、ある出来事の動向を前にして、その動向についての仮説の妥当性に対する事前確率（prior probability）と、その仮説のもとで得られる情報データによる条件付き確率（conditional probability）とから、ある結果が出たばあいに、元の仮説で得た情報データとの正しさぐあいとしての事後確率（posterior probability）を求めるための定理で、数学的にはべつだん難しくはない。
　ただし、ベイズの定理に入っている条件付き確率には、ちょっと注意を要する。条件付き確率は、いま予測しようとしている現象に対しての仮説がどのくらいありそうな「もっともらしさ」をもっているのかという、いわば「尤度」（likelihood）なのである。この「らしさ」の判定は人間の感じ方でしか出てこない。それにもかかわらず、ベイズの定理はこの条件を確率計算のなかに組みこんだ。

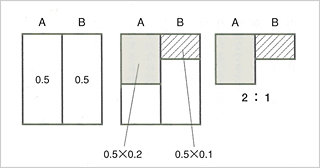
ベイズ理論による主観的心理的な推定のプロセス
製品ABを１回使用した場合の故障確率を求める
左：製品ABが次の１回の使用で故障する確率が五分五分であると仮定(事前確率)
中央：製品Aは5回に1回(0.2)、Bは10回に1回(0.1)故障すると仮定(条件的確率)
右：面積費から、Aは2/3、Bは1/3の確率で故障すると推定(事後確率)

　ここに確率論の愉快と不快とが交じるのである。とくに確率的予想に立ち会おうとする者たちをして、その多くを尤度というバイアスで悩ませることになる。
　悩ましさを逆手にとることも可能だ。実はベイズの定理は長いあいだそれほど重視されていなかったのだが、それが１０年ほど前だったか、２１世紀を迎えたときにビル・ゲイツが、「これからのマイクロソフト社の戦力はすべてベイズ・テクノロジーである」と明言したことから一挙に再注目を浴びるようになった。実際にもその前後から、ほとんどのスパム・メールの選別や、マイクロソフト社の文脈依存型検索エンジンや自然言語構文解析、グーグル社やオートノミー社のフィルタリングなどには、すべてベイズ・テクノロジーが応用された。
　しかし、ベイズ主義をどのように評価するかは、むしろ今後の問題である。ぼくはすでに指摘してきたように、ベイズ・テクノロジーの過信にはまたぞろ社会的なブラック・スワンを出現させかねない暗部が潜伏しているだろうと思っている。マイクロソフトもグーグルも、あまりにリスク回避的なのである。
　だから、それを多少は打破するためには、フラクタル型の確率モデルや、カオス型の思考方法や、さまざまな社会経済学的な思考方法の可能性もありうるだろうと思っている。ニクラス・ルーマンのシステム論やリバタリアニズム（自由至上主義）の思想にもヒントがあろう。

　話を株価に戻す。
　株価の確率はランダムウォーク・モデルのなかで説明されてきた。これは、株価の動きはすべて偶然の積み重ねによっているのだが、そこに、①市場が整備され、②経済指標（ファンダメンタルズ）や企業の情報開示が加わり、③市場参加者の合理的な参入があるのなら、市場はランダム・ウォークに近い姿をとるというモデルだった。
　ランダム・ウォークは、花粉粒子が水の中の水分子とぶつかって見せるブラウン運動とほぼ同じランダムな動きをすることをいう。株価の例でいえば、手元に入る情報が現在の株価に織りこまれているとすれば、今後の株価を動かすのは新しい情報だけだから、それが水分子となって花粉粒子としての株価をランダム・ウォークさせると見る。
　しかしこれは、株価が上がるか下がるかではなくて、その変動の記録のすべてはランダム・ウォークをしたのちに、たいてい正規分布に近付いていくという、ただそれだけのモデルである。
　だからランダムウォーク・モデルで短期の予想をすることは、ほとんどできない。けれども、ある程度の期間をとると、どんな変動でも正規分布に近くなる（ことが多い）。
　こういうモデルは理想的な市場の条件を想定することで成り立っている。市場は理想的であるはずがないので、金融市場の関係者たちは、ランダムウォーク・モデルがあてはまるように市場をたくみに陽動してきたわけである。それが過剰過多となって、結局はサブプライム・ローンの破綻問題などともなったのだが、それにもかかわらず、実際のトレーダーやファンドマネージャーの１０年間ほどの成績は、平均をとるとおおむね正規分布にそっているという意外な事実もあって、不確実な現象に向けて何かを予測するには、結局、このモデルに落ち着くということが多くなってきたのだった。
　とはいえこのモデルを容認しきるのは危険だ。ここにもフラクタル型やカオス型の、あるいは経済物理学的な変更が加わる必要がある。

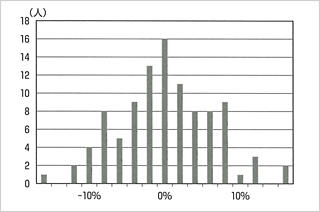
ファンドマネージャーの成績
正規曲線に従う年平均収益率の分布

　というわけで、市場と株価には偶然こそが関与していたはずなのである。それがわかるだけでも今夜の話は十分なのだが、実は株価だけではない。すべての不確実な動向には偶然が関与する。

　偶然をどのように哲学するかということは、イアン・ハッキングや木田元の千夜千冊でもその一端を書いておいたが、偶然を確率論とぶつけてみるといい。そう言っていいなら、そこには「見せかけの偶然」と「本当の偶然」があるからだ。
　「見せかけの偶然」は、駅で１０年ぶりの同級生にばったり会ったとか、天気予報も聞かないでなんとなく傘をもって出掛けたら雨が降ってきたとかといったことで、もしすべての情報を知り、すべてを計算できるなら、この偶然は「たまたま」ではなくて、たまたまに見えるだけだということになる。ここからは、確率とはたんに情報が不足している状態にのみ発生する一時的な概念だという考え方が生まれる。
　「本当の偶然」のほうは、たとえすべての状態を知り、すべての計算ができたとしても（つまり「ラプラスの魔」がいたとしても）、予測も制御もできない現象や事象のことをいう。このばあいは、その「たまたま」は客観的な確率だということで、つまらないネーミングだが統計学や確率論では「客観確率」などともいう。
　ということは「主観的確率」もあるわけで、それがさきほどのベイズの定理から発していたわけである。だから当然、ここには主観的なバイアスがかかっている。そういうバイアス入りの確率なのである。たとえば新発売の商品がヒットする確率などは、多くの者が経験や知識や情報にもとづいて予測をするもので、決して厳密なものではないけれども、そのようなヒットの予測が多かったということは、結局は確率の値に反映されてもいく。こういう場合は、関与者たちの期待値をこめたバイアスが確率の中に入りまじっているわけだ。

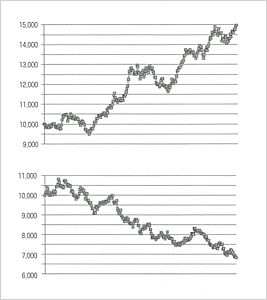
株価の動きと認知バイアス
図はランダム・ウォーク理論の仮定（全ったき偶然）のもと
コンピュータのシミュレーションで作り出した架空の株式市場
たまたまの株の値動きに上昇下降するトレンドを読んでしまう

　偶然は純粋な偶然ではいられなかったのだ。ということは、残された問題は、このように偶然に出入りするバイアスの正体とは何なのかということなのだが、本書ではそのあたりのことはまったくふれてはいない。

　本書にはいくつかのバイアスが紹介されている。そこにはいろいろな過誤が含まれる。
　バイアスで大きな影響力をもつとされているのは「認知バイアス」である。ランダムウォーク・モデルは人々の行動が合理的であることを前提にしているけれど、そんなことはむろんありえない。すべてに認知バイアスがかかっている。投資家のジョージ・ソロスはカール・ポパーにヒントを得て、それを「フレクシビリティ」として勘定に入れたわけだった。
　不確実性や偶然を相手にしすぎると、バイアスの中に自分が関与していることを忘れるだけではなく、そのうち気がつかないままに自己言及的な過誤を犯していることも少なくない。たとえばコイン投げのオモテが出る確率は５０パーセントであるはずなのに、続けてウラが７回も続けば、次にオモテが出るだろうと思いたくなるし、株価が連続して下がると、そろそろ上がるだろうとも思いたい。これは「ギャンブラーの誤謬」というもので、確率の解釈を自分で変更してしまっている。
　ここには自分が関与したんだからきっといいことがおこるだろうという、いわば「自己関与の幻想」という過誤もある。自分が詳しいつもりの会社の株価は欲目で見るものだし、自分が親しい相手との仕事はうまくいくと思うものなのだ。しかし、これはあやしい。
　なぜ、こういうふうになるかといえば、当事者の注意のカーソルが動かなくなるからだ。止まってしまうか、ゆらゆらする。これがいろいろのことをおこす。
　たとえば、めったにおこりそうもない発生の度合いの稀な現象のニュースのほうが、多くの人々に過大な注目をおこさせる。地震や同時テロや有名タレントの緊急逮捕などは、めったに起こらなくともどこかですぐにおこりそうな気がするし、もっと希有な現象でも、それがさかんにホラー映画やパニック映画のプロットとして頻繁にとりあげられているように、発生度が濃く見えて、ついつい勝手な確率解釈になっていく。
　これは「フレーミング効果」といわれるもので、注意のカーソルがシステムの内外を自在に動いていない。これでは問題のトータルな掴まえ方を失っていく。

　本書の著者によると、多くの投資家は自分ではそこそこうまくやっていると思いこんでいるらしい。また、自動車の運転感覚についてヒアリングをしてみると、たいていのドライバーは自分の運転技術を平均以上だと感じているともいう。
　これは「自己奉仕バイアス」である。ぼくはべつだんそういうことがあってもいっこうにいいと思っているのだが、これが投資や勧誘やキャンペーンのなかで強調されすぎると、けっこうヤバイことにもなっていく。
　企業の株価は、一株あたりの利益（純利益÷発行済株式数）の何倍になっているかで数値化される。これがＰＥＲ（株価収益率）とよばれる指標で、成長率の高い企業ではＰＥＲが高い。
　ある企業が成長力を市場で認められて、ＰＥＲ３０倍前後で取引されているとする。そのうち成長率が鈍化した。ところが、いったんＰＥＲ３０倍で取引されるようになった株価は、かんたんには変わらない。何年もたって鈍化や低迷が周知の事実になったころ、ＰＥＲが下がり始め、さらにその倍率が妥当ではないことが明々白々になると、突然に株価が大きく変動する。
　こういうものは「アンカーリング」というバイアスの一種で、いったん錨を投げて船を係留すると、そのアンカーの位置の値がしばらくじっとしてしまうという現象だ。投資市場ではしょっちゅう、株価の値をめぐってこのズレがおこっているという。ここには「自己正当化」がおこり、かつ、ある程度の進捗があったのちに心理学で「社会的証明」と名付けられている“横並び行動”に突然に移るということがおこっていく。
　こうして、これらがしだいに大同集約されたとき、投資市場における「ハーディング」（群衆化）になっていく。こうなると暴落がおこり、恐慌になりかねない。その逆になったとしても、それはバブルとなって、やっぱり空しくはじけてしまう。
　よくよく感ビジネスしたうえで、確率を相手にするべきなのだ。確率でわかることは少ないという警戒をするとともに、しかし長い目で見れば、確率的思考が社会の振幅をつくっていって、かまわないのである。
　こういう見方には金融トレーダーとして著者の譲れないところも随所に見えているのだが、それでもリスクについての悉無律（オンかオフかを決めるだけの規則）に偏っていく社会動向が過剰になってしまった昨今では、このような見方をする金融関係者はもっともっとふえていくべきである。

【参考情報】
（１）田渕直也の著書には、ほかに同じ日本実業出版社のものとして、『図解でわかるデリバティブのすべて』『図解でわかるランダムウォーク＆行動ファイナンスのすべて』『世界一やさしい金融工学の本です』『デリバティブのプロが教える金融基礎力要請講座』などがある。こういう金融工学おすすめ本の著者を、ぼくは今夜はいささか擁護したわけだが、その意図はもう少しこの連環篇がすすむと見えてくると思われたい。そこにはソロスやマンデルブロの金融工学批判だけではカバーできない問題があるからなのである。

（２）不確実性についての本はずいぶんあるが、そのことを情報論的確率論に結びつけたものとして、ぼくが最初のころに読んだのは金子郁容の『〈不確実性と情報〉入門』（岩波セミナーブックス）だった。金子さんに聞くと、いまでも大学の授業のテキストにけっこう使われているらしい。

（３）本書とほぼ同じ狙いをもったもので、もう少し本格的な著作として、小島寛之の『使える！ 確率的思考』（ちくま新書）、同じ著者の『確率的発想法』（ＮＨＫブックス）、神永正博の『統計思考力』（ディスカヴァー）などがある。さらに深い主旨で書かれたものには、スティーブン・センの『確率と統計のパラドックス』（青土社）がある。医学統計の世界の話だが、いろいろ身につまされる。もう少し哲学的になったものとしては、たとえばドナルド・ギリースの『確率の哲学理論』（日本経済評論社）などがある。